2004 Conference on Diff. Eqns. and Appl. in Math. Biology, Nanaimo, BC, Canada.
Electron. J. Diff. Eqns., Conference 12, 2005, pp. 57-64.

On the isospectral beams

Kazem Ghanbari

Abstract:
The free undamped infinitesimal transverse vibrations of a thin straight beam are modelled by a forth-order differential equation. This paper investigates the families of fourth-order systems which have one spectrum in common, and correspond to four different sets of end-conditions. The analysis is based on the transformation of the beam operator into a fourth-order self-adjoint linear differential operator. 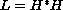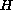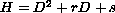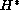This operator is factorized as a product $L=H^{*}H$, where $H$ is a second-order differential operator of the form $H=D^2+rD+s$, and $H^{*}$ is its adjoint operator.

Published April 20, 2005.
Math Subject Classifications: 34B05,34B10.
Key Words: Isospectral, Euler-Bernoulli equation for the vibrating beam, beam operator.

Show me the PDF file (192K), TEX file, and other files for this article.

Kazem Ghanbari
Department of Mathematics
Sahand University of Technology
Tabriz, Iran
email: kghanbari@sut.ac.ir

Return to the EJDE web page