2004 Conference on Diff. Eqns. and Appl. in Math. Biology, Nanaimo,
BC, Canada.
Electron. J. Diff. Eqns., Conference 12, 2005, pp. 79-85.
Continuous Newton method for star-like functions
Yakov Lutsky
Abstract:
We study a continuous analogue of Newton method for
solving the nonlinear equation
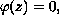
where
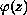 holomorphic function and
holomorphic function and
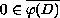 .
It is proved that this method converges, to the solution for each initial
data
.
It is proved that this method converges, to the solution for each initial
data
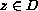 ,
if and only if
,
if and only if
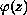 is a star-like function with
respect to either an interior or a boundary point.
Our study is based on the theory of one parameter continuous semigroups.
It enables us to consider convergence in the case of an interior as
well as a boundary location of the solution by the same approach.
is a star-like function with
respect to either an interior or a boundary point.
Our study is based on the theory of one parameter continuous semigroups.
It enables us to consider convergence in the case of an interior as
well as a boundary location of the solution by the same approach.
Published April 20, 2005.
Math Subject Classifications: 49M15, 46T25, 47H25.
Key Words: Newton method; star-like functions; continuous semigroup.
Show me the
PDF file (208K),
TEX file for this article.
 |
Yakov Lutsky
Department of Mathematics
Ort Braude College
Karmiel 21982, Israel
email: yalutsky@yahoo.com
|
|---|
Return to the EJDE web page
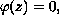
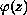 holomorphic function and
holomorphic function and
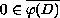 .
It is proved that this method converges, to the solution for each initial
data
.
It is proved that this method converges, to the solution for each initial
data
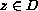 ,
if and only if
,
if and only if
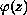 is a star-like function with
respect to either an interior or a boundary point.
Our study is based on the theory of one parameter continuous semigroups.
It enables us to consider convergence in the case of an interior as
well as a boundary location of the solution by the same approach.
is a star-like function with
respect to either an interior or a boundary point.
Our study is based on the theory of one parameter continuous semigroups.
It enables us to consider convergence in the case of an interior as
well as a boundary location of the solution by the same approach.
