2005-Oujda International Conference on Nonlinear Analysis,
Oujda, Morocco.
Electron. J. Diff. Eqns., Conference 14 (2006), pp. 9-20.
Existence result for variational degenerated parabolic problems
via pseudo-monotonicity
Lahsen Aharouch, Elhoussine Azroul, Mohamed Rhoudaf
Abstract:
In this paper, we study the existence of weak solutions for the
initial-boundary value problems of the nonlinear degenerated
parabolic equation
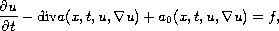
where
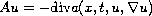 is a classical
divergence operator of Leray-lions acting from
is a classical
divergence operator of Leray-lions acting from
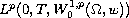 to its dual.
The source term
to its dual.
The source term
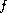 is assumed to belong to
is assumed to belong to
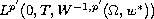 .
.
Published September 20, 2006.
Math Subject Classifications: 35J60.
Key Words: Weighted Sobolev spaces; boundary value problems;
truncations; parabolic problems.
Show me the
PDF file (244K),
TEX file, and other files for this article.
 |
Lahsen Aharouch
Département de Mathématiques et Informatique
Faculté des Sciences Dhar-Mahraz
B.P 1796 Atlas Fès, Maroc
email: l_aharouch@yahoo.fr
|
|---|
 |
Elhoussine Azroul
Département de Mathématiques et Informatique
Faculté des Sciences Dhar-Mahraz
B.P 1796 Atlas Fès, Maroc
email: azroul_elhoussine@yahoo.fr
|
|---|
 |
Mohamed Rhoudaf
Département de Mathématiques et Informatique
Faculté des Sciences Dhar-Mahraz
B.P 1796 Atlas Fès, Maroc
email: rhoudaf_mohamed@yahoo.fr
|
|---|
Return to the table of contents for this conference.
Return to the EJDE web page
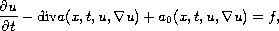
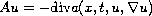 is a classical
divergence operator of Leray-lions acting from
is a classical
divergence operator of Leray-lions acting from
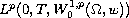 to its dual.
The source term
to its dual.
The source term
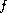 is assumed to belong to
is assumed to belong to
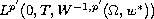 .
.


