In this work we study the existence of a positive solutions to the non homogeneous equation
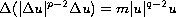
with Navier boundary conditions, where
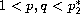 and
and
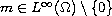 ,
,
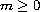 .
In the case
.
In the case
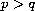 and
and
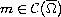 ,
we prove the uniqueness of this solution.
,
we prove the uniqueness of this solution.
Mohamed Talbi, Najib Tsouli
Abstract:
In this work we study the existence of a positive solutions to the
non homogeneous equation
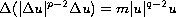
with Navier boundary conditions, where
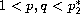 and
and
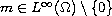 ,
,
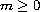 .
In the case
.
In the case
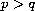 and
and
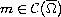 ,
we prove the uniqueness of this solution.
,
we prove the uniqueness of this solution.
Math Subject Classifications: 35J60, 35J30, 35J65.
Key Words: Ekeland's principle; p-biharmonic operator;
Palais-Smale condition.
Published September 20, 2006. Show me the PDF file (239K), TEX file, and other files for this article.
 |
Mohamed Talbi Département de Mathématiques et Informatique Faculté des Sciences, Université Mohamed 1er Oujda, Maroc email: talbi_md@yahoo.fr |
|---|---|
 |
Najib Tsouli University Mohamed 1er, Faculty of sciences Department of Mathematics, Oujda, Morocco e-mail: tsouli@sciences.univ-oujda.ac.ma |
Return to the table of contents for this conference.
Return to the EJDE web page