Sixth Mississippi State Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 15 (2007), pp. 51-65.
Existence and non-existence results for a nonlinear heat equation
Canan Celik
Abstract:
In this study, we consider the
nonlinear heat equation
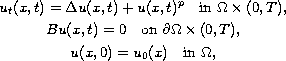
with Dirichlet and mixed boundary conditions, where
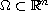 is a smooth bounded domain
and
is a smooth bounded domain
and
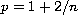 is the critical exponent.
For an initial condition
is the critical exponent.
For an initial condition
 ,
we prove the non-existence
of local solution in
,
we prove the non-existence
of local solution in
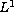 for
the mixed boundary condition. Our proof is based on comparison
principle for Dirichlet and mixed boundary value problems. We also
establish the global existence in
for
the mixed boundary condition. Our proof is based on comparison
principle for Dirichlet and mixed boundary value problems. We also
establish the global existence in
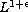 to the Dirichlet
problem, for any fixed
to the Dirichlet
problem, for any fixed
 with
with
 sufficiently small.
sufficiently small.
Published February 28, 2007.
Math Subject Classifications: 35K55, 35K05, 35K57, 35B33.
Key Words: Nonlinear heat equation; mixed boundary condition;
global existence; critical exponent.
Show me the
PDF file (275K),
TEX file for this article.
 |
Canan Celik
Departmane to Mathematics
TOBB Economics and Technology University
Sögütözü cad. No. 43. 06560 Sögütözü
Ankara, Turkey
email: canan.celik@etu.edu.tr |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
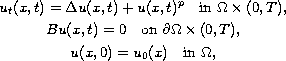
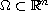 is a smooth bounded domain
and
is a smooth bounded domain
and
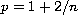 is the critical exponent.
For an initial condition
is the critical exponent.
For an initial condition
 ,
we prove the non-existence
of local solution in
,
we prove the non-existence
of local solution in
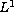 for
the mixed boundary condition. Our proof is based on comparison
principle for Dirichlet and mixed boundary value problems. We also
establish the global existence in
for
the mixed boundary condition. Our proof is based on comparison
principle for Dirichlet and mixed boundary value problems. We also
establish the global existence in
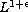 to the Dirichlet
problem, for any fixed
to the Dirichlet
problem, for any fixed
 with
with
 sufficiently small.
sufficiently small.
