Sixth Mississippi State Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 15 (2007), pp. 229-238.
Global attractivity in a nonlinear difference equation
Chuanxi Qian, Yijun Sun
Abstract:
In this paper, we study the asymptotic behavior of positive
solutions of the nonlinear difference equation
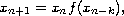
where
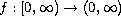 is a unimodal
function, and
is a unimodal
function, and
 is a nonnegative integer. Sufficient
conditions for the positive equilibrium to be a global attractor
of all positive solutions are established. Our results can be
applied to to some difference equations derived from mathematical
biology.
is a nonnegative integer. Sufficient
conditions for the positive equilibrium to be a global attractor
of all positive solutions are established. Our results can be
applied to to some difference equations derived from mathematical
biology.
Published February 28, 2007.
Math Subject Classifications: 39A10.
Key Words: Nonlinear difference equation; global attractor;
unimodal function; positive equilibrium.
Show me the
PDF file (233K),
TEX file for this article.
 |
Chuanxi Qian
Department of Mathematics and Statistics
Mississippi State University
Mississippi State, MS 39762, USA
email: qian@math.msstate.edu |
|---|
 |
Yijun Sun
Department of Mathematics and Statistics
Mississippi State University
Mississippi State, MS 39762, USA
email: ys101@msstate.edu |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
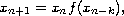
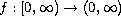 is a unimodal
function, and
is a unimodal
function, and
 is a nonnegative integer. Sufficient
conditions for the positive equilibrium to be a global attractor
of all positive solutions are established. Our results can be
applied to to some difference equations derived from mathematical
biology.
is a nonnegative integer. Sufficient
conditions for the positive equilibrium to be a global attractor
of all positive solutions are established. Our results can be
applied to to some difference equations derived from mathematical
biology.

