2006 International Conference in honor of Jacqueline Fleckinger.
Electron. J. Diff. Eqns., Conference 16 (2007), pp. 15-28.
Nonlinear multidimensional parabolic-hyperbolic equations
Gloria Aguilar, Laurent Levi, Monique Madaune-Tort
Abstract:
This paper deals with the coupling of a quasilinear parabolic
problem with a first order hyperbolic one in a multidimensional
bounded domain
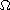 . In a region
. In a region
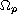 a
diffusion-advection-reaction type equation is set while in the
complementary
a
diffusion-advection-reaction type equation is set while in the
complementary
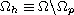 ,
only advection-reaction terms are taken into account.
Suitable transmission conditions at the interface
,
only advection-reaction terms are taken into account.
Suitable transmission conditions at the interface
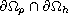 are required. We find a weak solution characterized by an entropy
inequality on the whole domain.
are required. We find a weak solution characterized by an entropy
inequality on the whole domain.
Published May 15, 2007.
Math Subject Classifications: 35F25, 35K65.
Key Words: Coupling problem; degenerate parabolic-hyperbolic equation;
entropy solution.
Show me the
PDF file (275K),
TEX file for this article.
 |
Gloria Aguilar
Departamento de Matemática Aplicada
Universidad de Zaragoza, CPS
Maria de Luna 3,
E-50018 Zaragoza, Spain
email: gaguilar@unizar.es |
|---|
 |
Laurent Lévi
Laboratoire de Mathématiques Appliquées, UMR 5142
Université de Pau, IPRA, BP 1155
F-64013 Pau Cedex, France
email: laurent.levi@univ-pau.fr |
|---|
 |
Monique Madaune-Tort
Laboratoire de Mathématiques Appliquées, UMR 5142
Université de Pau, IPRA, BP 1155
F-64013 Pau Cedex, France
email: monique.madaune-tort@univ-pau.fr |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
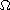 . In a region
. In a region
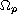 a
diffusion-advection-reaction type equation is set while in the
complementary
a
diffusion-advection-reaction type equation is set while in the
complementary
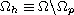 ,
only advection-reaction terms are taken into account.
Suitable transmission conditions at the interface
,
only advection-reaction terms are taken into account.
Suitable transmission conditions at the interface
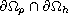 are required. We find a weak solution characterized by an entropy
inequality on the whole domain.
are required. We find a weak solution characterized by an entropy
inequality on the whole domain.


