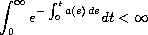Seventh Mississippi State - UAB Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 17 (2009), pp. 33-38
Second-order differential equations with asymptotically small
dissipation and piecewise flat potentials
Alexandre Cabot, Hans Engler, Sebastien Gadat
Abstract:
We investigate the asymptotic properties as
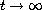 of the differential equation
of the differential equation

where
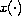 is
is
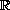 -valued,
the map
-valued,
the map
 is non increasing, and
is non increasing, and
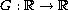 is a potential with locally Lipschitz
continuous derivative. We identify conditions on the function
is a potential with locally Lipschitz
continuous derivative. We identify conditions on the function
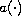 that guarantee or exclude the convergence of solutions of this problem
to points in
that guarantee or exclude the convergence of solutions of this problem
to points in
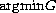 ,
in the case where
,
in the case where
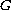 is
convex and
is
convex and
 is an interval. The condition
is an interval. The condition
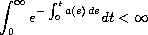
is known to be necessary for convergence of trajectories. We give a
slightly stronger condition that is sufficient.
Published April 15, 2009.
Math Subject Classifications: 34G20, 34A12, 34D05.
Key Words: Differential equation; dissipative dynamical system;
vanishing damping; asymptotic behavior.
Show me the PDF file (213 KB),
TEX file for this article.
 |
Alexandre Cabot
Département de Mathématiques, Université Montpellier II,
CC 051
Place Eugène Bataillon, 34095 Montpellier Cedex 5, France
email: acabot@math.univ-montp2.fr
|
|---|
 |
Hans Engler
Department of Mathematics, Georgetown University
Box 571233
Washington, DC 20057, USA
email: engler@georgetown.edu
|
|---|
 |
Sébastien Gadat
Institut de Mathématiques de Toulouse, Université Paul Sabatier
118, Route de Narbonne 31062 Toulouse Cedex 9, France
email: Sebastien.Gadat@math.ups-tlse.fr
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
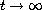 of the differential equation
of the differential equation

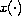 is
is
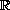 -valued,
the map
-valued,
the map
 is non increasing, and
is non increasing, and
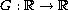 is a potential with locally Lipschitz
continuous derivative. We identify conditions on the function
is a potential with locally Lipschitz
continuous derivative. We identify conditions on the function
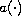 that guarantee or exclude the convergence of solutions of this problem
to points in
that guarantee or exclude the convergence of solutions of this problem
to points in
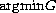 ,
in the case where
,
in the case where
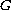 is
convex and
is
convex and
 is an interval. The condition
is an interval. The condition