Seventh Mississippi State - UAB Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 17 (2009), pp. 39-49.
A boundary control problem with a nonlinear reaction term
John R. Cannon, Mohamed Salman
Abstract:
The authors study the problem
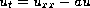 ,
,
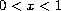 ,
,
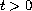 ;
;
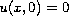 , and
, and
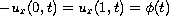 ,
where
,
where
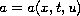 , and
, and
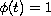 for
for
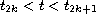 and
and
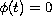 for
for
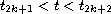 ,
,
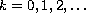 with
with
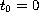 and the sequence
and the sequence
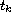 is determined by the equations
is determined by the equations
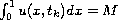 , for
, for
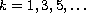 ,
and
,
and
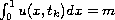 , for
, for
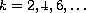 ,
where
,
where
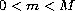 .
Note that the switching points
.
Note that the switching points
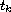 , are unknown.
A maximum principal argument has been used to prove that the solution
is positive under certain conditions. Existence and uniqueness are
demonstrated. Theoretical estimates of the
, are unknown.
A maximum principal argument has been used to prove that the solution
is positive under certain conditions. Existence and uniqueness are
demonstrated. Theoretical estimates of the
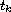 and
and
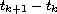 are obtained and numerical verifications of the estimates are
presented.
are obtained and numerical verifications of the estimates are
presented.
Published April 15, 2009.
Math Subject Classifications: 35K57, 35K55.
Key Words: Reaction-diffusion, Parabolic, Nonlocal boundary conditions.
Show me the PDF file (321 KB),
TEX file for this article.
 |
John R. Cannon
University of Central Florida, Department of Mathematics
Orlando, FL 32816, USA
email: jcannon@pegasus.cc.ucf.edu
|
|---|
 |
Mohamed Salman
Tuskegee University, Department of Mathematics
Tuskegee, AL 36088, USA
email: msalmanz@gmail.com
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
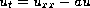 ,
,
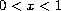 ,
,
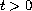 ;
;
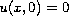 , and
, and
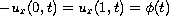 ,
where
,
where
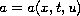 , and
, and
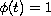 for
for
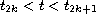 and
and
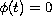 for
for
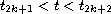 ,
,
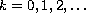 with
with
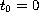 and the sequence
and the sequence
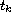 is determined by the equations
is determined by the equations
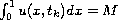 , for
, for
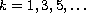 ,
and
,
and
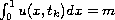 , for
, for
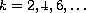 ,
where
,
where
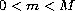 .
Note that the switching points
.
Note that the switching points
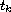 , are unknown.
A maximum principal argument has been used to prove that the solution
is positive under certain conditions. Existence and uniqueness are
demonstrated. Theoretical estimates of the
, are unknown.
A maximum principal argument has been used to prove that the solution
is positive under certain conditions. Existence and uniqueness are
demonstrated. Theoretical estimates of the
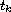 and
and
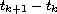 are obtained and numerical verifications of the estimates are
presented.
are obtained and numerical verifications of the estimates are
presented.

