Seventh Mississippi State - UAB Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 17 (2009), pp. 185-195.
Regularity of solutions to doubly nonlinear diffusion equations
Jochen Merker
Abstract:
We prove under weak assumptions that solutions
 of
doubly nonlinear reaction-diffusion equations
of
doubly nonlinear reaction-diffusion equations
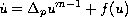
to initial values
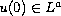 are instantly regularized to functions
are instantly regularized to functions
 (ultracontractivity). Our proof is
based on a priori estimates of
(ultracontractivity). Our proof is
based on a priori estimates of
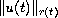 for a time-dependent exponent
for a time-dependent exponent
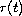 .
These a priori estimates can be obtained in an
elementary way from logarithmic Gagliardo-Nirenberg inequalities
by an optimal choice of
.
These a priori estimates can be obtained in an
elementary way from logarithmic Gagliardo-Nirenberg inequalities
by an optimal choice of
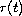 ,
and they do not only imply
ultracontractivity, but provide further information about the
long-time behaviour.
,
and they do not only imply
ultracontractivity, but provide further information about the
long-time behaviour.
Published April 15, 2009.
Math Subject Classifications: 35K65, 35B35, 46E35, 35B45.
Key Words: p-Laplacian; doubly nonlinear evolution equations;
ultracontractive semigroups;
logarithmic Gagliardo-Nirenberg inequalities.
Show me the PDF file (219 KB),
TEX file for this article.
 |
Jochen Merker
University of Rostock, D-18051 Rostock, Germany
email: jochen.merker@uni-rostock.de
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
 of
doubly nonlinear reaction-diffusion equations
of
doubly nonlinear reaction-diffusion equations
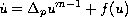
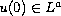 are instantly regularized to functions
are instantly regularized to functions
 (ultracontractivity). Our proof is
based on a priori estimates of
(ultracontractivity). Our proof is
based on a priori estimates of
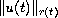 for a time-dependent exponent
for a time-dependent exponent
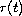 .
These a priori estimates can be obtained in an
elementary way from logarithmic Gagliardo-Nirenberg inequalities
by an optimal choice of
.
These a priori estimates can be obtained in an
elementary way from logarithmic Gagliardo-Nirenberg inequalities
by an optimal choice of
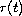 ,
and they do not only imply
ultracontractivity, but provide further information about the
long-time behaviour.
,
and they do not only imply
ultracontractivity, but provide further information about the
long-time behaviour.
