2007 Conference on Variational and Topological Methods: Theory, Applications,
Numerical Simulations, and Open Problems.
Electron. J. Diff. Eqns., Conference 18 (2010), pp. 23-31.
Oddness of least energy nodal solutions on radial domains
Christopher Grumiau, Christophe Troestler
Abstract:
In this article, we consider the Lane-Emden problem
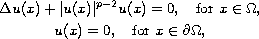
where
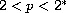 and
and
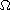 is a ball or an annulus in
is a ball or an annulus in
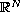 ,
,
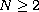 .
We show that, for p
close to 2, least energy nodal solutions are odd with
respect to an hyperplane --
which is their nodal surface. The proof ingredients are a
constrained implicit function theorem and the fact that the second
eigenvalue is simple up to rotations.
.
We show that, for p
close to 2, least energy nodal solutions are odd with
respect to an hyperplane --
which is their nodal surface. The proof ingredients are a
constrained implicit function theorem and the fact that the second
eigenvalue is simple up to rotations.
Published July 10, 2010.
Math Subject Classifications: 35J20, 35A30.
Key Words: Variational method; least energy nodal solution; symmetry;
oddness; (nodal) Nehari manifold; Bessel functions; Laplace-Beltrami
operator on the sphere; implicit function theorem.
Show me the PDF file (238K),
TEX file for this article.
Christopher Grumiau
Institut de Mathématique,
Université de Mons
Place du Parc, 20,
B-7000 Mons, Belgium
email: Christopher.Grumiau@umons.ac.be
|
Christophe Troestler
Institut de Mathématique,
Université de Mons
Place du Parc, 20,
B-7000 Mons, Belgium
email: Christophe.Troestler@umons.ac.be
|
Return to the table of contents
for this conference.
Return to the EJDE web page
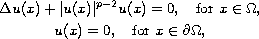
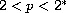 and
and
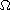 is a ball or an annulus in
is a ball or an annulus in
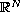 ,
,
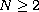 .
We show that, for p
close to 2, least energy nodal solutions are odd with
respect to an hyperplane --
which is their nodal surface. The proof ingredients are a
constrained implicit function theorem and the fact that the second
eigenvalue is simple up to rotations.
.
We show that, for p
close to 2, least energy nodal solutions are odd with
respect to an hyperplane --
which is their nodal surface. The proof ingredients are a
constrained implicit function theorem and the fact that the second
eigenvalue is simple up to rotations.