Eighth Mississippi State - UAB Conference on Differential Equations
and Computational Simulations.
Electron. J. Diff. Eqns., Conference 19 (2010), pp. 99-121.
Continuous dependence of solutions for ill-posed evolution problems
Matthew Fury, Rhonda J. Hughes
Abstract:
We prove Holder-continuous dependence results for the difference
between certain ill-posed and well-posed evolution problems in
a Hilbert space. Specifically, given a positive self-adjoint
operator D in a Hilbert space, we consider the ill-posed evolution
problem
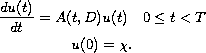
We determine functions
![$f:[0,T]\times [0,\infty)\to \mathbb{R}$](gifs/ab.gif) for which solutions of the well-posed problem
for which solutions of the well-posed problem

approximate known solutions of the original ill-posed problem,
thereby establishing continuous dependence on modelling for
the problems under consideration.
Published September 25, 2010.
Math Subject Classifications: 47A52, 42C40.
Key Words: Continuous dependence on modelling; time-dependent problems;
Ill-posed problems.
Show me the PDF file (312K),
TEX file for this article.
 |
Matthew Fury
Department of Mathematics, Bryn Mawr College
Bryn Mawr, PA 19010, USA
email: mfury@brynmawr.edu
|
|---|
 |
Rhonda J. Hughes
Department of Mathematics, Bryn Mawr College
Bryn Mawr, PA 19010, USA
email: rhughes@brynmawr.edu
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
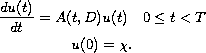
![$f:[0,T]\times [0,\infty)\to \mathbb{R}$](gifs/ab.gif) for which solutions of the well-posed problem
for which solutions of the well-posed problem


