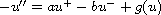Ninth MSU-UAB Conference on Differential Equations and Computational Simulations. Electron. J. Diff. Eqns., Conference 20 (2013), pp. 103-117.

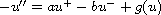A Landesman-Lazer condition for the boundary-value problem $-u''=a u^+ - b u^- +g(u)$ with periodic boundary conditions

Quinn A. Morris, Stephen B. Robinson

Abstract:
In this article we prove the existence of solutions for the boundary-value problem
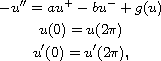
$$\displaylines{ -u''=a u^+ - b u^- +g(u)\cr u(0)=u(2 \pi)\cr u'(0)=u'(2 \pi), }$$
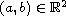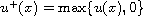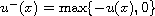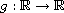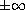where $(a,b)\in \mathbb{R}^2$, $u^+ (x) = \max \{u(x),0\}$, $u^- (x) = \max \{-u(x),0\}$, and $g: \mathbb{R} \to \mathbb{R}$ is a bounded, continuous function. We consider both the resonance and nonresonance cases relative to the Fucik Spectrum. For the resonance case we assume a generalized Landesman-Lazer condition that depends upon the average values of g at $\pm\infty$. Our theorems generalize the results in [1] by removing certain restrictions on (a,b). Our proofs are also different in that they rely heavily on a variational characterization of the Fucik Spectrum given in [3].

Published October 31, 2013.
Math Subject Classifications: 34B15.
Key Words: Fucik spectrum; resonance; Landesman-Lazer condition; variational approach.

Show me the PDF file (264 K), TEX file, and other files for this article.

Quinn A. Morris
Department of Mathematics and Statistics
The University of North Carolina at Greensboro
116 Petty Building, 317 College Avenue
Greensboro, NC 27412, USA
email: qamorris@uncg.edu
Stephen B. Robinson
Department of Mathematics, Wake Forest University
PO Box 7388, 127 Manchester Hall
Winston-Salem, NC 27109, USA
email: sbr@wfu.edu

Return to the table of contents for this conference.
Return to the EJDE web page