Variational and Topological Methods: Theory, Applications,
Numerical Simulations, and Open Problems.
Electron. J. Diff. Eqns., Conference 21 (2014), pp. 45-59.
Elliptic problems on the space of weighted with the distance to the
boundary integrable functions revisited
Jesus Idelfonso Diaz, Jean-Michel Rakotoson
Abstract:
We revisit the regularity of very weak solution to second-order elliptic
equations Lu=f in
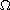 with u=0 on
with u=0 on
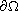 for
for
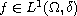 ,
,
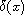 the distance to the boundary
the distance to the boundary
 .
While doing this, we extend our previous results
(and many others in the literature) by allowing the presence of
distributions f+g which are more general than Radon measures
(more precisely with g in the dual of suitable Lorentz-Sobolev spaces)
and by making weaker assumptions on the coefficients of L.
One of the new tools is a Hardy type inequality developed
recently by the second author. Applications to the study of the gradient
of solutions of some singular semilinear equations are also given.
.
While doing this, we extend our previous results
(and many others in the literature) by allowing the presence of
distributions f+g which are more general than Radon measures
(more precisely with g in the dual of suitable Lorentz-Sobolev spaces)
and by making weaker assumptions on the coefficients of L.
One of the new tools is a Hardy type inequality developed
recently by the second author. Applications to the study of the gradient
of solutions of some singular semilinear equations are also given.
Published February 10, 2014.
Math Subject Classifications: 35J25, 35J60, 35P30, 35J67.
Key Words: Very weak solutions; semilinear elliptic equations;
distance to the boundary; weighted spaces measure;
Hardy inequalities; Hardy spaces.
Show me the PDF(271 K) file for this article.
TEX file for this article.
TEX and other files for this article.-->
 |
Jesús Idelfonso Díaz
Instituto de Matemática Interdisciplinar
and Departamento de Matemática Aplicada
Universidad Complutense de Mmadrid
Plaza de las Ciencias No. 3, 28040 Madrid, Spain
email: diaz.racefyn@insde.es
|
|---|
 |
Jean-Michel Rakotoson
Laboratoire de Mathématiques et Applications
Université de Poitiers
Boulevard Marie et Pierre Curie, Teleport 2, BP 30179
86962 Futuroscope Chasseneuil Cedex, France
email: rako@math.univ-poitiers.fr
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
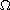 with u=0 on
with u=0 on
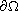 for
for
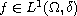 ,
,
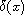 the distance to the boundary
the distance to the boundary
 .
While doing this, we extend our previous results
(and many others in the literature) by allowing the presence of
distributions f+g which are more general than Radon measures
(more precisely with g in the dual of suitable Lorentz-Sobolev spaces)
and by making weaker assumptions on the coefficients of L.
One of the new tools is a Hardy type inequality developed
recently by the second author. Applications to the study of the gradient
of solutions of some singular semilinear equations are also given.
.
While doing this, we extend our previous results
(and many others in the literature) by allowing the presence of
distributions f+g which are more general than Radon measures
(more precisely with g in the dual of suitable Lorentz-Sobolev spaces)
and by making weaker assumptions on the coefficients of L.
One of the new tools is a Hardy type inequality developed
recently by the second author. Applications to the study of the gradient
of solutions of some singular semilinear equations are also given.

