Variational and Topological Methods: Theory, Applications,
Numerical Simulations, and Open Problems.
Electron. J. Diff. Eqns., Conference 21 (2014), pp. 61-76.
Symmetry analysis and numerical solutions for semilinear elliptic systems
C. Tyler Diggans, John M. Neuberger, James W. Swift
Abstract:
We study a two-parameter family of so-called Hamiltonian
systems defined on a region
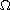 in
in
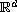 with the bifurcation parameters
with the bifurcation parameters
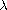 and
and
 of the form:
of the form:
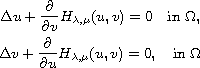
taking
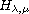 to be a function of two variables satisfying certain
conditions. We use numerical methods adapted from Automated Bifurcation
Analysis for Nonlinear Elliptic Partial Difference Equations on Graphs
(Inter. J. Bif. Chaos, 2009) to approximate solution pairs.
After providing a symmetry analysis of the solution space of pairs of
functions defined on the unit square, we numerically approximate bifurcation
surfaces over the two dimensional parameter space. A cusp catastrophe
is found on the diagonal in the parameter space where
to be a function of two variables satisfying certain
conditions. We use numerical methods adapted from Automated Bifurcation
Analysis for Nonlinear Elliptic Partial Difference Equations on Graphs
(Inter. J. Bif. Chaos, 2009) to approximate solution pairs.
After providing a symmetry analysis of the solution space of pairs of
functions defined on the unit square, we numerically approximate bifurcation
surfaces over the two dimensional parameter space. A cusp catastrophe
is found on the diagonal in the parameter space where
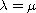 and is
explained in terms of symmetry breaking bifurcation. Finally, we suggest
a more theoretical direction for our future work on this topic.
and is
explained in terms of symmetry breaking bifurcation. Finally, we suggest
a more theoretical direction for our future work on this topic.
Published February 10, 2014.
Math Subject Classifications: 35J15, 65N30.
Key Words: Nonlinear elliptic PDE; elliptic systems; Newton's method;
GNGA; bifurcation.
Show me the PDF(920 K),
TEX file for this article.
 |
C. Tyler Diggans
Department of Mathematics
Northern Arizona University, 86005
Flagstaff, AZ 86011, USA
email: Tyler.Diggans@nau.edu
|
|---|
 |
John M. Neuberger
Department of Mathematics
Northern Arizona University, 86005
Flagstaff, AZ 86011, USA
email: John.Neuberger@nau.edu
|
|---|
| |
Jim W. Swift
Department of Mathematics
Northern Arizona University, 86005
Flagstaff, Arizona, USA
email: Jim.Swift@nau.edu
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
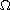 in
in
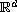 with the bifurcation parameters
with the bifurcation parameters
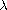 and
and
 of the form:
of the form:
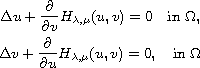
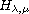 to be a function of two variables satisfying certain
conditions. We use numerical methods adapted from Automated Bifurcation
Analysis for Nonlinear Elliptic Partial Difference Equations on Graphs
(Inter. J. Bif. Chaos, 2009) to approximate solution pairs.
After providing a symmetry analysis of the solution space of pairs of
functions defined on the unit square, we numerically approximate bifurcation
surfaces over the two dimensional parameter space. A cusp catastrophe
is found on the diagonal in the parameter space where
to be a function of two variables satisfying certain
conditions. We use numerical methods adapted from Automated Bifurcation
Analysis for Nonlinear Elliptic Partial Difference Equations on Graphs
(Inter. J. Bif. Chaos, 2009) to approximate solution pairs.
After providing a symmetry analysis of the solution space of pairs of
functions defined on the unit square, we numerically approximate bifurcation
surfaces over the two dimensional parameter space. A cusp catastrophe
is found on the diagonal in the parameter space where
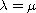 and is
explained in terms of symmetry breaking bifurcation. Finally, we suggest
a more theoretical direction for our future work on this topic.
and is
explained in terms of symmetry breaking bifurcation. Finally, we suggest
a more theoretical direction for our future work on this topic.

