International Conference on Applications of Mathematics to Nonlinear Sciences.
Electron. J. Diff. Eqns., Conference 24 (2017), pp. 1-10.
Existence results for multivalued operators of monotone type in reflexive
Banach spaces
Dhruba R. Adhikari
Abstract:
Let
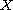 be a real reflexive Banach space and
be a real reflexive Banach space and
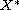 its dual space.
Let
its dual space.
Let
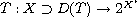 be an operator of class
be an operator of class
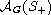 ,
where
,
where
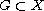 .
A result concerning the existence of pathwise
connected sets in the range of T is established, and as a consequence,
an open mapping theorem is proved. In addition, for certain operators
T of class
.
A result concerning the existence of pathwise
connected sets in the range of T is established, and as a consequence,
an open mapping theorem is proved. In addition, for certain operators
T of class
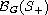 ,
the existence of nonzero solutions of
,
the existence of nonzero solutions of
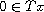 in
in
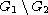 ,
where
,
where
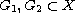 satisfy
satisfy
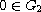 and
and
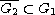 ,
is established. The Skrypnik's topological
degree theory is used, utilizing approximating schemes for operators
of classes
,
is established. The Skrypnik's topological
degree theory is used, utilizing approximating schemes for operators
of classes
 and
and
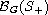 ,
along with the methodology of a recent invariance of domain result by Kartsatos
and the author.
,
along with the methodology of a recent invariance of domain result by Kartsatos
and the author.
Published November 15, 2017.
Math Subject Classifications: 47H14, 47H05, 47H11.
Key Words: Browder and Skrypnik degree theory; invariance of domain;
nonzero solutions; bounded demicontinuous operator of type (S+).
Show me the PDF file (224 K),
TEX file for this article.
 |
Dhruba R. Adhikari
Department of Mathematics
Kennesaw State University
Georgia 30060, USA
email: dadhikar@kennesaw.edu
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
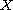 be a real reflexive Banach space and
be a real reflexive Banach space and
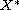 its dual space.
Let
its dual space.
Let
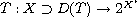 be an operator of class
be an operator of class
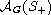 ,
where
,
where
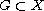 .
A result concerning the existence of pathwise
connected sets in the range of T is established, and as a consequence,
an open mapping theorem is proved. In addition, for certain operators
T of class
.
A result concerning the existence of pathwise
connected sets in the range of T is established, and as a consequence,
an open mapping theorem is proved. In addition, for certain operators
T of class
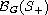 ,
the existence of nonzero solutions of
,
the existence of nonzero solutions of
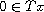 in
in
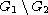 ,
where
,
where
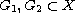 satisfy
satisfy
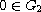 and
and
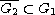 ,
is established. The Skrypnik's topological
degree theory is used, utilizing approximating schemes for operators
of classes
,
is established. The Skrypnik's topological
degree theory is used, utilizing approximating schemes for operators
of classes
 and
and
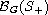 ,
along with the methodology of a recent invariance of domain result by Kartsatos
and the author.
,
along with the methodology of a recent invariance of domain result by Kartsatos
and the author.
