Two nonlinear days in Urbino 2017.
Electron. J. Diff. Eqns., Conference 25 (2018), pp. 1-13.
Infinitely many small energy solutions for a fractional Kirchhoff
equation involving sublinear nonlinearities
Vincenzo Ambrosio
Abstract:
This article is devoted to the study of the following fractional Kirchhoff
equation
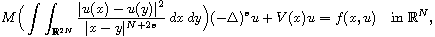
where
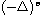 is the fractional Laplacian,
is the fractional Laplacian,
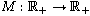 is the Kirchhoff term,
is the Kirchhoff term,
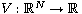 is a positive continuous potential and f(x, u)
is only locally defined for |u| small.
By combining a variant of the symmetric Mountain Pass with a Moser iteration
argument, we prove the existence of infinitely many weak solutions converging
to zero in
is a positive continuous potential and f(x, u)
is only locally defined for |u| small.
By combining a variant of the symmetric Mountain Pass with a Moser iteration
argument, we prove the existence of infinitely many weak solutions converging
to zero in
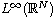 -norm.
-norm.
Published September 15, 2018.
Math Subject Classifications: 47G20, 35R11, 35A15, 58E05.
Key Words: Fractional Kirchhoff equation; sublinear nonlinearity;
symmetric mountain pass.
Show me the PDF file (279 K),
TEX and other files for this article.
 |
Vincenzo Ambrosio
Dipartimento di Scienze Pure e Applicate (DiSPeA)
Università degli Studi di Urbino "Carlo Bo"
Piazza della Repubblica, 13
61029 Urbino (Pesaro e Urbino, Italy)
email: vincenzo.ambrosio@uniurb.it
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
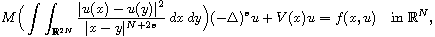
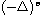 is the fractional Laplacian,
is the fractional Laplacian,
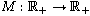 is the Kirchhoff term,
is the Kirchhoff term,
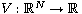 is a positive continuous potential and f(x, u)
is only locally defined for |u| small.
By combining a variant of the symmetric Mountain Pass with a Moser iteration
argument, we prove the existence of infinitely many weak solutions converging
to zero in
is a positive continuous potential and f(x, u)
is only locally defined for |u| small.
By combining a variant of the symmetric Mountain Pass with a Moser iteration
argument, we prove the existence of infinitely many weak solutions converging
to zero in
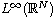 -norm.
-norm.
