We study the existence, uniqueness and multiplicity for the sublinear fractional problem
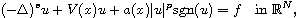
where
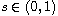 ,
,
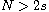 ,
,
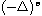 is the fractional Laplacian,
is the fractional Laplacian,
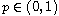 ,
,
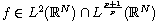 ,
,
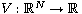 and
and
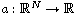 are positive bounded functions.
are positive bounded functions.
Teresa Isernia
Abstract:
We study the existence, uniqueness and multiplicity for the sublinear
fractional problem
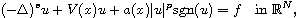
where
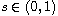 ,
,
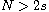 ,
,
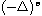 is the fractional Laplacian,
is the fractional Laplacian,
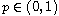 ,
,
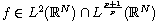 ,
,
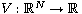 and
and
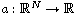 are positive bounded functions.
are positive bounded functions.
Published September 15, 2018.
Math Subject Classifications: 35A15, 35J60, 35R11.
Key Words: Fractional Laplacian; sublinear growth; variational methods.
Show me the PDF file (275 K), TEX and other files for this article.
 |
Teresa Isernia Dipartimento di Ingegneria Industriale e Scienze Matematiche Università Politecnica delle Marche Via Brecce Bianche, 12 60131 Ancona, Italy email: teresa.isernia@unina.it |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page