2021 UNC Greensboro PDE Conference.
Electron. J. Diff. Eqns., Conference 26 (2022), pp. 45-58.
On the L^2-orthogonality of Steklov eigenfunctions
Manki Cho, Mauricio A. Rivas
Abstract:
This article analyzes the interior
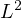 -orthogonality of the Steklov eigenfunctions
on rectangles
-orthogonality of the Steklov eigenfunctions
on rectangles
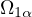 .
It is shown that most Steklov eigenfunctions are, indeed, pairwise orthogonal in
.
It is shown that most Steklov eigenfunctions are, indeed, pairwise orthogonal in
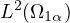 , and pairs that are not orthogonal are nearly orthogonal.
Explicit formulae for exact inner products in
, and pairs that are not orthogonal are nearly orthogonal.
Explicit formulae for exact inner products in
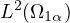 of the eigenfunctions are found, and to elucidate the intricate formulae obtained,
accompanying numerics are provided.
Then envelopes that bound the calculated inner products are constructed that simplify
the convoluted formulae.
This leads to a straightforward description of the nearly orthogonal Steklov eigenfunctions.
A consequence of the calculations is a tabulation of the mean value of Steklov
eigenfunctions over
of the eigenfunctions are found, and to elucidate the intricate formulae obtained,
accompanying numerics are provided.
Then envelopes that bound the calculated inner products are constructed that simplify
the convoluted formulae.
This leads to a straightforward description of the nearly orthogonal Steklov eigenfunctions.
A consequence of the calculations is a tabulation of the mean value of Steklov
eigenfunctions over
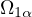 .
.
Published August 25, 2022.
Math Subject Classifications: 35P05, 31A20, 35J05.
Key Words: Harmonic functions; Steklov eigenfunctions; Laplacian eigenfunctions.
DOI: https://doi.org/10.58997/ejde.conf.26.c1
Show me the PDF file (488 K),
TEX file for this article.
 |
Manki Cho
Department of Mathematics and Statistics
University of Houston - Clear Lake
2700 Bay Area Blvd
Houston, TX 77058, USA
email: cho@uhcl.edu
|
|---|
 |
Mauricio A. Rivas
Department of Mathematics and Statistics
North Carolina A&T State University
1601 East Market Street
Greensboro, NC 27411, USA
email: marivas@ncat.edu
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
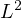 -orthogonality of the Steklov eigenfunctions
on rectangles
-orthogonality of the Steklov eigenfunctions
on rectangles
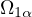 .
It is shown that most Steklov eigenfunctions are, indeed, pairwise orthogonal in
.
It is shown that most Steklov eigenfunctions are, indeed, pairwise orthogonal in
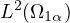 , and pairs that are not orthogonal are nearly orthogonal.
Explicit formulae for exact inner products in
, and pairs that are not orthogonal are nearly orthogonal.
Explicit formulae for exact inner products in
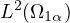 of the eigenfunctions are found, and to elucidate the intricate formulae obtained,
accompanying numerics are provided.
Then envelopes that bound the calculated inner products are constructed that simplify
the convoluted formulae.
This leads to a straightforward description of the nearly orthogonal Steklov eigenfunctions.
A consequence of the calculations is a tabulation of the mean value of Steklov
eigenfunctions over
of the eigenfunctions are found, and to elucidate the intricate formulae obtained,
accompanying numerics are provided.
Then envelopes that bound the calculated inner products are constructed that simplify
the convoluted formulae.
This leads to a straightforward description of the nearly orthogonal Steklov eigenfunctions.
A consequence of the calculations is a tabulation of the mean value of Steklov
eigenfunctions over
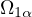 .
.

