Special Issue in honor of Alan C. Lazer.
Electron. J. Diff. Eqns., Special Issue 01 (2021), pp. 293-300.
Existence and multiplicity results for p-q-Laplacian boundary value problems
Ananta Acharya, Ujjal Das, Ratnasingham Shivaji
Abstract:
We study positive solutions to the boundary value problem
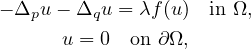
where
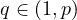 and Ω is a bounded domain in
and Ω is a bounded domain in
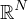 , N >1
with smooth boundary, λ is a positive parameter,
and
, N >1
with smooth boundary, λ is a positive parameter,
and
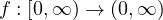 is C1, nondecreasing, and p-sublinear at
infinity i.e.
is C1, nondecreasing, and p-sublinear at
infinity i.e.
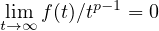 .
We discuss existence and multiplicity results for classes of such f.
Further, when N=1, we discuss an example which exhibits S-shaped bifurcation curves.
.
We discuss existence and multiplicity results for classes of such f.
Further, when N=1, we discuss an example which exhibits S-shaped bifurcation curves.
DOI: https://doi.org/10.58997/ejde.sp.01.a3
Published January 18, 2022.
Math Subject Classifications: 35J70, 35J55.
Key Words: Multiple positive solutions; p-q Laplacian; sub-super solution.
Show me the PDF file (453 K),
TEX file for this article.
 |
Ananta Acharya
Department of Mathematics and Statistics
University of North Carolina at Greensboro
Greensboro, NC 27412, USA
email: a_achary@uncg.edu
|
|---|
 |
Ujjal Das
Technion-Israel Institute of Technology
Haifa-32000, Israel
email: ujjaldas@campus.technion.ac.il, ujjal.rupam.das@gmail.com
|
|---|
 |
Ratnasingham Shivaji
Department of Mathematics and Statistics
University of North Carolina at Greensboro
Greensboro, NC 27412, USA
email: r_shivaj@uncg.edu
|
|---|
Return to the table of contents
for this special issue.
Return to the EJDE web page
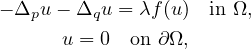
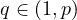 and Ω is a bounded domain in
and Ω is a bounded domain in
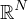 , N >1
with smooth boundary, λ is a positive parameter,
and
, N >1
with smooth boundary, λ is a positive parameter,
and
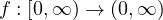 is C1, nondecreasing, and p-sublinear at
infinity i.e.
is C1, nondecreasing, and p-sublinear at
infinity i.e.
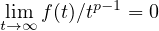 .
We discuss existence and multiplicity results for classes of such f.
Further, when N=1, we discuss an example which exhibits S-shaped bifurcation curves.
.
We discuss existence and multiplicity results for classes of such f.
Further, when N=1, we discuss an example which exhibits S-shaped bifurcation curves.


