We study analytic smooth solutions of a general, strongly parabolic semilinear Cauchy problem of 2m-th order in
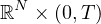 with analytic coefficients (in space and time variables)
and analytic initial data (in space variables).
They are expressed in terms of holomorphic continuation of
global (weak) solutions to the system valued in
a suitable Besov interpolation space of
with analytic coefficients (in space and time variables)
and analytic initial data (in space variables).
They are expressed in terms of holomorphic continuation of
global (weak) solutions to the system valued in
a suitable Besov interpolation space of
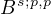 -type
at every time moment
-type
at every time moment
![$t\in [0,T]$](images/a2x.png) .
Given
.
Given
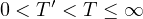 ,
it is proved that any
,
it is proved that any
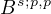 -type solution
-type solution
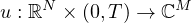 with analytic initial data possesses a bounded holomorphic continuation
with analytic initial data possesses a bounded holomorphic continuation
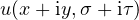 into a complex domain in
into a complex domain in
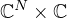 defined by
defined by
 ,
,
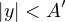 and
and
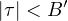 ,
where
,
where
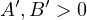 are constants depending upon T'.
The proof uses the extension of a weak solution to a
are constants depending upon T'.
The proof uses the extension of a weak solution to a
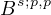 -type solution in a domain in
-type solution in a domain in
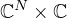 , such that this extension
satisfies the Cauchy-Riemann equations.
The holomorphic extension is obtained with a help from
holomorphic semigroups and maximal regularity theory for
parabolic problems in Besov interpolation spaces of
, such that this extension
satisfies the Cauchy-Riemann equations.
The holomorphic extension is obtained with a help from
holomorphic semigroups and maximal regularity theory for
parabolic problems in Besov interpolation spaces of
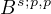 -type imbedded (densely and continuously) into
an
-type imbedded (densely and continuously) into
an
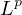 -type Lebesgue space.
Applications include risk models
for European options in Mathematical Finance.
-type Lebesgue space.
Applications include risk models
for European options in Mathematical Finance.
DOI: https://doi.org/10.58997/ejde.sp.01.b1

