The spread of an infectious disease which confers immunity after recovery from infection, can be described by a SIR model, i.e. a system of three differential equations for the dependent variables
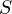 ,
,
 , and
, and
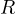 , which are the numbers (densities) of susceptible,
infectious and recovered (immune) individuals, respectively.
The equations for
, which are the numbers (densities) of susceptible,
infectious and recovered (immune) individuals, respectively.
The equations for
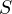 and
and
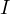 are typically nonlinear.
In this article, we consider two spatio-temporal SIR models.
The first model is similar to reaction-diffusion systems in chemistry.
A simple birth-and-death process is incorporated, and it is assumed, that a fraction f of the newborns is vaccinated and is then immune for life.
We show how the smallest eigenvalue of the eigenvalue problem associated with the
linearized equation for I is related to the basic reproduction number
are typically nonlinear.
In this article, we consider two spatio-temporal SIR models.
The first model is similar to reaction-diffusion systems in chemistry.
A simple birth-and-death process is incorporated, and it is assumed, that a fraction f of the newborns is vaccinated and is then immune for life.
We show how the smallest eigenvalue of the eigenvalue problem associated with the
linearized equation for I is related to the basic reproduction number
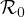 ,
a key concept in the mathematical theory of infectious diseases.
Here it is defined by a variational principle.
We show that the disease-free equilibrium is asymptotically stable if
,
a key concept in the mathematical theory of infectious diseases.
Here it is defined by a variational principle.
We show that the disease-free equilibrium is asymptotically stable if
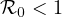 ,
or if
,
or if
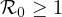 and
and
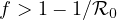 , and unstable if
, and unstable if
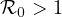 and
and
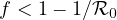 .
In the other model we assume that the population consists of sedentary individuals
who leave their home only temporarily. Both models suggest that restriction of mobility may
be counterproductive for the control of an epidemic outbreak.
.
In the other model we assume that the population consists of sedentary individuals
who leave their home only temporarily. Both models suggest that restriction of mobility may
be counterproductive for the control of an epidemic outbreak.

