Special Issue in honor of Alan C. Lazer.
Electron. J. Diff. Eqns., Special Issue 01 (2021), pp. 327-344.
Generalized quasilinear equations with critical growth and nonlinear boundary conditions
Liliane de Almeida Maia, Jose Carlos Oliveira Junior, Ricardo Ruviaro
Abstract:
We study the quasilinear problem

where
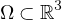 is a bounded domain with
regular boundary
is a bounded domain with
regular boundary
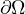 ,
,
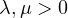 ,
,
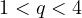 ,
,
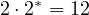 ,
,
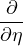 is the outer normal derivative and g has a
subcritical growth in the sense of the trace Sobolev embedding. We prove a regularity
result for all weak solutions for a modified, and
introducing a new type of constraint, we obtain a multiplicity of solutions,
including the existence of a ground state.
is the outer normal derivative and g has a
subcritical growth in the sense of the trace Sobolev embedding. We prove a regularity
result for all weak solutions for a modified, and
introducing a new type of constraint, we obtain a multiplicity of solutions,
including the existence of a ground state.
Published June 27, 2022.
Math Subject Classifications: 35J25, 35J62, 35B33.
Key Words: Quasilinear equations; variational methods; concave nonlinearities critical exponent; ground state solution.
DOI: https://doi.org/10.58997/ejde.sp.01.m3
Show me the PDF file (396 K),
TEX file for this article.
 |
Liliane de A. Maia
Universidade de Brasília
Departamento de Matemática, 70.910-900
Brasília, DF, Brazil
email: lilimaia@unb.br
|
|---|
 |
José Carlos Oliveira Junior
Universidade Federal do Tocantins
Departamento de Matemática, 77.824-838
Araguaína, TO, Brazil
email: jc.oliveira@uft.edu.br
|
|---|
 |
Ricardo Ruviaro
Universidade de Brasília
Departamento de Matemática, 70.910-900
Brasília, DF, Brazil
email: ruviaro@unb.br
|
|---|
Return to the table of contents
for this special issue.
Return to the EJDE web page

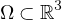 is a bounded domain with
regular boundary
is a bounded domain with
regular boundary
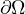 ,
,
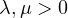 ,
,
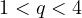 ,
,
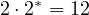 ,
,
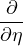 is the outer normal derivative and g has a
subcritical growth in the sense of the trace Sobolev embedding. We prove a regularity
result for all weak solutions for a modified, and
introducing a new type of constraint, we obtain a multiplicity of solutions,
including the existence of a ground state.
is the outer normal derivative and g has a
subcritical growth in the sense of the trace Sobolev embedding. We prove a regularity
result for all weak solutions for a modified, and
introducing a new type of constraint, we obtain a multiplicity of solutions,
including the existence of a ground state.


