Special Issue in honor of Alan C. Lazer.
Electron. J. Diff. Eqns., Special Issue 01 (2021), pp. 183-202.
An asymmetric problem at resonance with a one-sided Ahmad-Lazer-Paul condition
Leandro L. Recova, Adolfo J. Rumbos
Abstract:
In this article, we study the semilinear elliptic boundary value problem

where
 denotes the negative part of
denotes the negative part of
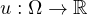 ;
;
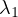 is the first eigenvalue of the N-dimensional Laplacian with Dirichlet boundary conditions
in a connected, open, bounded set
is the first eigenvalue of the N-dimensional Laplacian with Dirichlet boundary conditions
in a connected, open, bounded set
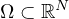 ,
,
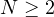 ; and
; and
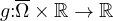 is a continuous function.
Assuming a one-sided Ahmad-Lazer-Paul condition, we establish conditions for existence
and multiplicity of solutions by using variational methods
and infinite-dimensional Morse Theory.
is a continuous function.
Assuming a one-sided Ahmad-Lazer-Paul condition, we establish conditions for existence
and multiplicity of solutions by using variational methods
and infinite-dimensional Morse Theory.
Published October 6, 2021.
Math Subject Classifications: 35J20.
Key Words: Resonance; critical groups; Morse theory; Ekeland's variational principle.
DOI: https://doi.org/10.58997/ejde.sp.01.r2
Show me the PDF file (397 K),
TEX file for this article.
 |
Leandro L. Recôva
T-Mobile Inc.,
Ontario, California 91761, USA
email leandro.recova3@t-mobile.com
|
|---|
 |
Adolfo J. Rumbos
Department of Mathematics
Pomona College
Claremont, California 91711, USA
email: arumbos@pomona.edu
|
|---|
Return to the table of contents
for this special issue.
Return to the EJDE web page

 denotes the negative part of
denotes the negative part of
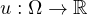 ;
;
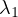 is the first eigenvalue of the N-dimensional Laplacian with Dirichlet boundary conditions
in a connected, open, bounded set
is the first eigenvalue of the N-dimensional Laplacian with Dirichlet boundary conditions
in a connected, open, bounded set
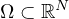 ,
,
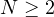 ; and
; and
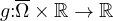 is a continuous function.
Assuming a one-sided Ahmad-Lazer-Paul condition, we establish conditions for existence
and multiplicity of solutions by using variational methods
and infinite-dimensional Morse Theory.
is a continuous function.
Assuming a one-sided Ahmad-Lazer-Paul condition, we establish conditions for existence
and multiplicity of solutions by using variational methods
and infinite-dimensional Morse Theory.

