Special Issue in honor of John W. Neuberger.
Electron. J. Diff. Eqns., Special Issue 02 (2023), pp. 1-10.
A nonexistence result for p-Laplacian systems in a ball
Abraham Abebe, Maya Chhetri
Abstract:
We consider the p-Laplacian system
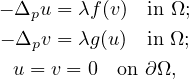
where λ>0 is a parameter,
 is the p-Laplacian
operator for p>1 and Ω is a unit ball in
is the p-Laplacian
operator for p>1 and Ω is a unit ball in
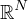 (N≥2).
The nonlinearities
(N≥2).
The nonlinearities
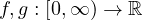 are assumed to be
are assumed to be
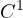 strictly increasing semipositone functions (f(0)< 0 and g(0)<0) that are
p-superlinear at infinity.
By analyzing the solution in the interior of the unit ball as well as near the boundary,
we prove that the system has no positive
radially symmetric and radially decreasing solution for λ large.
strictly increasing semipositone functions (f(0)< 0 and g(0)<0) that are
p-superlinear at infinity.
By analyzing the solution in the interior of the unit ball as well as near the boundary,
we prove that the system has no positive
radially symmetric and radially decreasing solution for λ large.
Published March 27, 2023.
Math Subject Classifications: 34B18, 35B09, 35J92.
Key Words: Positive radial solution; ball; p-Laplacian system;
semipositone; p-superlinear at infinity.
DOI: https://doi.org/10.58997/ejde.sp.02.a1
Show me the PDF file (346 K),
TEX file for this article.
 |
Abraham Abebe
Department of Science, Technology, Engineering & Mathematics
Delaware County Community College
PA 19122 USA
email: aabebe@dccc.edu
|
|---|
 |
Maya Chhetri
Department of Mathematics and Statistics
The University of North Carolina at Greensboro
Greensboro, NC 27402 USA
email: maya@uncg.edu
|
|---|
Return to the table of contents
for this special issue.
Return to the EJDE web page
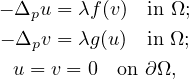
 is the p-Laplacian
operator for p>1 and Ω is a unit ball in
is the p-Laplacian
operator for p>1 and Ω is a unit ball in
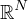 (N≥2).
The nonlinearities
(N≥2).
The nonlinearities
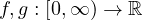 are assumed to be
are assumed to be
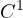 strictly increasing semipositone functions (f(0)< 0 and g(0)<0) that are
p-superlinear at infinity.
By analyzing the solution in the interior of the unit ball as well as near the boundary,
we prove that the system has no positive
radially symmetric and radially decreasing solution for λ large.
strictly increasing semipositone functions (f(0)< 0 and g(0)<0) that are
p-superlinear at infinity.
By analyzing the solution in the interior of the unit ball as well as near the boundary,
we prove that the system has no positive
radially symmetric and radially decreasing solution for λ large.

