Special Issue in honor of John W. Neuberger.
Electron. J. Diff. Eqns., Special Issue 02 (2023), pp. 209-230.
Fucik spectrum with weights and existence of solutions for nonlinear
elliptic equations with nonlinear boundary conditions
Nsoki Mavinga, Quinn A. Morris, Stephen B. Robinson
Abstract:
We consider the boundary value problem
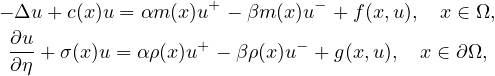
where
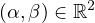 ,
,
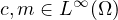 ,
,
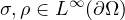 , and the nonlinearities f and g
are bounded continuous functions.
We study the asymmetric (Fucik) spectrum with weights, and prove existence theorems
for nonlinear perturbations of this spectrum for both the resonance and non-resonance cases.
For the resonance case, we provide a sufficient condition, the so-called generalized
Landesman-Lazer condition, for the solvability. The proofs are based on variational methods
and rely strongly on the variational characterization of the spectrum.
, and the nonlinearities f and g
are bounded continuous functions.
We study the asymmetric (Fucik) spectrum with weights, and prove existence theorems
for nonlinear perturbations of this spectrum for both the resonance and non-resonance cases.
For the resonance case, we provide a sufficient condition, the so-called generalized
Landesman-Lazer condition, for the solvability. The proofs are based on variational methods
and rely strongly on the variational characterization of the spectrum.
Published March 27, 2023.
Math Subject Classifications: 35P30, 35J60, 35J66.
Key Words: Fucik Spectrum; resonance; nonlinear boundary condition.
DOI: https://doi.org/10.58997/ejde.sp.02.m2
Show me the PDF file (405 K),
TEX file for this article.
 |
Nsoki Mavinga
Department of Mathematics & Statistics
Swarthmore College
Swarthmore, PA 19081-1390, USA
email: nmaving1@swarthmore.edu
|
|---|
 |
Quinn A. Morris
Department of Mathematical Sciences
Appalachian State University
Boone, NC 28608, USA
email: morrisqa@appstate.edu
|
|---|
 |
Stephen B. Robinson
Department of Mathematics
Wake Forest University
Winston-Salem, NC 27109, USA
email: sbr@wfu.edu
|
|---|
Return to the table of contents
for this special issue.
Return to the EJDE web page
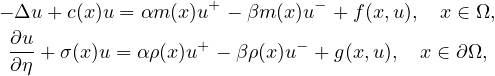
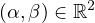 ,
,
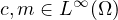 ,
,
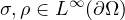 , and the nonlinearities f and g
are bounded continuous functions.
We study the asymmetric (Fucik) spectrum with weights, and prove existence theorems
for nonlinear perturbations of this spectrum for both the resonance and non-resonance cases.
For the resonance case, we provide a sufficient condition, the so-called generalized
Landesman-Lazer condition, for the solvability. The proofs are based on variational methods
and rely strongly on the variational characterization of the spectrum.
, and the nonlinearities f and g
are bounded continuous functions.
We study the asymmetric (Fucik) spectrum with weights, and prove existence theorems
for nonlinear perturbations of this spectrum for both the resonance and non-resonance cases.
For the resonance case, we provide a sufficient condition, the so-called generalized
Landesman-Lazer condition, for the solvability. The proofs are based on variational methods
and rely strongly on the variational characterization of the spectrum.


