Special Issue in honor of John W. Neuberger.
Electron. J. Diff. Eqns., Special Issue 02 (2023), pp. 231-238.
Existence of positive global radial solutions to nonlinear elliptic systems
Seshadev Padhi, Julio G. Dix
Abstract:
In this article we obtain global positive and radially symmetric solutions
to the system of nonlinear elliptic equations
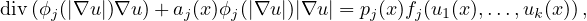
and in particular to Laplace's equation
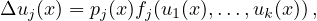
where
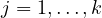 ,
,
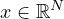 ,
,
 ,
,
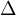 is the Laplacian operator, and
is the Laplacian operator, and
 is the gradient.
Also we state conditions for solutions to be bounded, and to be unbounded.
With an example we illustrate our results.
is the gradient.
Also we state conditions for solutions to be bounded, and to be unbounded.
With an example we illustrate our results.
Published March 27, 2023.
Math Subject Classifications: 35J25, 45F10, 35B08.
Key Words: Radial solution; elliptic system.
DOI: https://doi.org/10.58997/ejde.sp.02.p1
Show me the PDF file (338 K),
TEX file for this article.
 |
Seshadev Padhi
Department of Mathematics
Birla Institute of Technology
Mesra Ranchi, India
email: spadhi@bitmesra.ac.in
|
|---|
 |
Julio G. Dix
Department of Mathematics
Texas State University
601 University Drive
San Marcos, TX 78666, USA
email: jd01@txstate.edu
|
|---|
Return to the table of contents
for this special issue.
Return to the EJDE web page
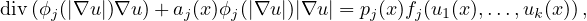
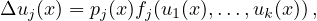
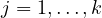 ,
,
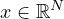 ,
,
 ,
,
 is the Laplacian operator, and
is the Laplacian operator, and
 is the gradient.
Also we state conditions for solutions to be bounded, and to be unbounded.
With an example we illustrate our results.
is the gradient.
Also we state conditions for solutions to be bounded, and to be unbounded.
With an example we illustrate our results.

