This article studies the asymptotic behavior of solutions to the damped, non-linear wave equation

which is known as degenerate if the greatest lower bound for
 is zero, and non-degenerate if the greatest lower bound is positive.
For the non-degenerate case, it is already known that solutions decay
exponentially, but for the degenerate case exponential decay has remained
an open question. In an attempt to answer this question,
we show that in general solutions can not decay with exponential order,
but that
is zero, and non-degenerate if the greatest lower bound is positive.
For the non-degenerate case, it is already known that solutions decay
exponentially, but for the degenerate case exponential decay has remained
an open question. In an attempt to answer this question,
we show that in general solutions can not decay with exponential order,
but that
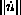 is square integrable on
is square integrable on
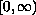 .
We extend our results to systems and to related equations.
.
We extend our results to systems and to related equations.
