Electron. J. Diff. Eqns., Vol. 1999(1999), No. 48, pp. 1-8.
On the smallness of the (possible) singular set in space for
3D Navier-Stokes equations
Zoran Grujic
Abstract:
We utilize
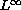 estimates on the complexified solutions of 3D
Navier-Stokes equations via a plurisubharmonic measure type maximum principle
to give a short proof of the fact that the Hausdorff dimension of the
(possible) singular set in space is less or equal 1 assuming chaotic,
Cantor set-like structure of the blow-up profile.
estimates on the complexified solutions of 3D
Navier-Stokes equations via a plurisubharmonic measure type maximum principle
to give a short proof of the fact that the Hausdorff dimension of the
(possible) singular set in space is less or equal 1 assuming chaotic,
Cantor set-like structure of the blow-up profile.
Submitted August 20, 1999. Published December 3, 1999.
Math Subject Classifications: 35Q30, 76D03.
Key Words: Navier-Stokes equations, singular
set, turbulence.
Show me the
PDF file (111K),
TEX file for this article.
Zoran Grujic
Department of Mathematics
University of Texas
Austin, TX 78712, USA
e-mail: grujic@math.utexas.edu
Return to the EJDE web page
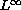 estimates on the complexified solutions of 3D
Navier-Stokes equations via a plurisubharmonic measure type maximum principle
to give a short proof of the fact that the Hausdorff dimension of the
(possible) singular set in space is less or equal 1 assuming chaotic,
Cantor set-like structure of the blow-up profile.
estimates on the complexified solutions of 3D
Navier-Stokes equations via a plurisubharmonic measure type maximum principle
to give a short proof of the fact that the Hausdorff dimension of the
(possible) singular set in space is less or equal 1 assuming chaotic,
Cantor set-like structure of the blow-up profile.