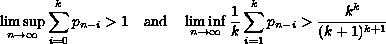Electron. J. Diff. Eqns., Vol. 2001(2001), No. 10, pp. 1-15.
Oscillation criteria for delay difference equations
Jianhua Shen & I. P. Stavroulakis
Abstract:
This paper is concerned with the oscillation of
all solutions of the delay difference equation
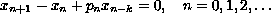
where
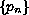 is a sequence of nonnegative real numbers and
is a sequence of nonnegative real numbers and
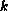 is a
positive integer. Some new oscillation conditions are established. These
conditions concern the case when none
of the well-known oscillation conditions
is a
positive integer. Some new oscillation conditions are established. These
conditions concern the case when none
of the well-known oscillation conditions
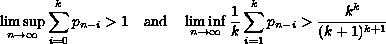
is satisfied.
Submitted January 9, 2001. Published January 23, 2001.
Math Subject Classifications: 39A10.
Key Words: Oscillation, non-oscillation, delay difference equation.
Show me the
PDF file (143K),
TEX file for this article.
|
Jianhua Shen
Department of Mathematics
Hunan Normal University
Changsha, Hunan 410081, China
e-mail: jhsh@public.cs.hn.cn |
|---|
 |
Ioannis P. Stavroulakis
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
e-mail: ipstav@cc.uoi.gr |
|---|
Return to the EJDE web page
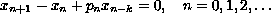
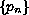 is a sequence of nonnegative real numbers and
is a sequence of nonnegative real numbers and
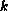 is a
positive integer. Some new oscillation conditions are established. These
conditions concern the case when none
of the well-known oscillation conditions
is a
positive integer. Some new oscillation conditions are established. These
conditions concern the case when none
of the well-known oscillation conditions