Electron. J. Diff. Eqns., Vol. 2001(2001), No. 67, pp. 1-13.
Stabilization of linear continuous time-varying systems
with state delays in Hilbert spaces
Vu Ngoc Phat
Abstract:
This paper studies the stabilization of the infinite-dimensional
linear time-varying system with state delays
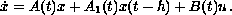
The operator
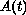 is assumed to be the generator of
a strong evolution operator. In contrast to the previous results,
the stabilizability conditions are obtained via solving a Riccati
differential equation and do not involve any stability property
of the evolution operator. Our conditions are easy to construct
and to verify. We provide a step-by-step procedure for finding
feedback controllers and state stability conditions for some
linear delay control systems with nonlinear perturbations.
is assumed to be the generator of
a strong evolution operator. In contrast to the previous results,
the stabilizability conditions are obtained via solving a Riccati
differential equation and do not involve any stability property
of the evolution operator. Our conditions are easy to construct
and to verify. We provide a step-by-step procedure for finding
feedback controllers and state stability conditions for some
linear delay control systems with nonlinear perturbations.
Submitted August 16, 2001. Published October 19, 2001.
Math Subject Classifications: 93D15, 93B05, 34K20.
Key Words: Stabilization, time-varying, delay system, Riccati equation.
Show me the
PDF file (240K),
TEX file for this article.
 |
Vu Ngoc Phat
School of Electrical Engineering & Telecommunications
Faculty of Engineering, University of New South Wales
Sydney 2052, Australia
e-mail: phvu@syscon.ee.unsw.edu.au
On leave from
Institute of Mathematics
P.O. Box 631, BoHo, Hanoi, Vietnam
e-mail:vnphat@thevinh.ncst.ac.vn |
|---|
Return to the EJDE web page
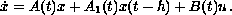
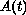 is assumed to be the generator of
a strong evolution operator. In contrast to the previous results,
the stabilizability conditions are obtained via solving a Riccati
differential equation and do not involve any stability property
of the evolution operator. Our conditions are easy to construct
and to verify. We provide a step-by-step procedure for finding
feedback controllers and state stability conditions for some
linear delay control systems with nonlinear perturbations.
is assumed to be the generator of
a strong evolution operator. In contrast to the previous results,
the stabilizability conditions are obtained via solving a Riccati
differential equation and do not involve any stability property
of the evolution operator. Our conditions are easy to construct
and to verify. We provide a step-by-step procedure for finding
feedback controllers and state stability conditions for some
linear delay control systems with nonlinear perturbations.
