Electron. J. Diff. Eqns., Vol. 2003(2003), No. 33, pp. 1-25.
Analytic solution to a class of integro-differential equations
Xuming Xie
Abstract:
In this paper, we consider the integro-differential equation
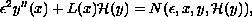
where
![${cal H}(y)[x]=\frac{1}{\pi}(P)\int_{-\infty}^{\infty}
\frac{y(t)}{t-x}dt$](gifs/ab.gif) is the Hilbert transform.
The existence and uniqueness of analytic solution in appropriately
chosen space is proved. Our method consists of extending the
equation to an appropriately chosen region in the complex plane,
then use the Contraction Mapping Theorem.
is the Hilbert transform.
The existence and uniqueness of analytic solution in appropriately
chosen space is proved. Our method consists of extending the
equation to an appropriately chosen region in the complex plane,
then use the Contraction Mapping Theorem.
Submitted August 13, 2002. Published March 28, 2003.
Math Subject Classifications: 34A20, 45E05.
Key Words: Analytic solution, singular integro-differential equation.
Show me the
PDF file (309K),
TEX file for this article.
 |
Xuming Xie
Department of Mathematical Sciences
University of Delaware
501 Ewing Hall
Newark, DE 19716, USA
email: xie@math.udel.edu |
|---|
Return to the EJDE web page
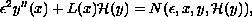
![${cal H}(y)[x]=\frac{1}{\pi}(P)\int_{-\infty}^{\infty}
\frac{y(t)}{t-x}dt$](gifs/ab.gif) is the Hilbert transform.
The existence and uniqueness of analytic solution in appropriately
chosen space is proved. Our method consists of extending the
equation to an appropriately chosen region in the complex plane,
then use the Contraction Mapping Theorem.
is the Hilbert transform.
The existence and uniqueness of analytic solution in appropriately
chosen space is proved. Our method consists of extending the
equation to an appropriately chosen region in the complex plane,
then use the Contraction Mapping Theorem.
