This article concerns the nonnegative solutions to the Cauchy problem
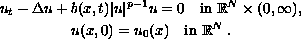
We investigate how the comparison principle, extinction in finite time, instantaneous shrinking of support, and existence of solutions depend on the behaviour of the coefficient
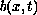 .
.
Junjie Li
Abstract:
This article concerns the nonnegative solutions to the Cauchy problem
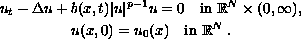
We investigate how the comparison principle, extinction
in finite time, instantaneous shrinking of support,
and existence of solutions depend on the behaviour of
the coefficient
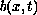 .
.
Submitted December 5, 2002. Published April 8, 2004.
Math Subject Classifications: 35B05, 35K55.
Key Words: Comparison principle, extinction, shrinking of support,
existence.
Show me the PDF file (260K), TEX file for this article.
 |
Junjie Li Department of Mathematicas, Yuquan Campus Zhejiang University, Hangzhou 310027, China email: ljj@math.zju.edu.cn |
|---|
Return to the EJDE web page