Electron. J. Diff. Eqns., Vol. 2004(2004), No. 56, pp. 1-15.
Positive solutions for a class of quasilinear singular equations
Jose Valdo Goncalves & Carlos Alberto P. Santos
Abstract:
This article concerns the existence and uniqueness of solutions to the
quasilinear equation
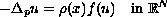
with
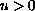 and
and
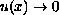 as
as
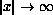 .
Here
.
Here
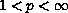 ,
,
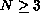 ,
,
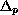 is the
is the
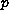 -Laplacian
operator,
-Laplacian
operator,
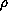 and
and
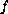 are positive functions, and
are positive functions, and
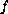 is singular at 0. Our approach uses fixed point arguments,
the shooting method, and a lower-upper solutions argument.
is singular at 0. Our approach uses fixed point arguments,
the shooting method, and a lower-upper solutions argument.
Submitted October 6, 2003. Published April 13, 2004.
Math Subject Classifications: 35B40, 35J25, 35J60.
Key Words: Singular equations, radial positive solutions, fixed points,
shooting method, lower-upper solutions
Show me the
PDF file (275K),
TEX file for this article.
 |
Jose Valdo Goncalves
Universidade de Brasilia
Departamento de Matematica
70910-900 Brasilia, DF, Brasil
email: jv0ag@unb.br |
|---|
 |
Carlos Alberto P. Santos
Universidade Federal de Goias
Departamento de Matematica
Catalao, GO, Brasil
email: csantos@unb.br |
|---|
Return to the EJDE web page
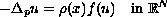
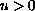 and
and
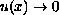 as
as
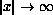 .
Here
.
Here
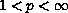 ,
,
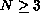 ,
,
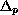 is the
is the
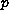 -Laplacian
operator,
-Laplacian
operator,
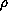 and
and
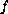 are positive functions, and
are positive functions, and
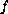 is singular at 0. Our approach uses fixed point arguments,
the shooting method, and a lower-upper solutions argument.
is singular at 0. Our approach uses fixed point arguments,
the shooting method, and a lower-upper solutions argument.

