Electron. J. Diff. Eqns., Vol. 2005(2005), No. 125, pp. 1-13.
Decay of solutions to equations modelling incompressible bipolar
non-newtonian fluids
Bo-Qing Dong
Abstract:
This article concerns systems of equations
that model incompressible bipolar non-Newtonian fluid motion
in the whole space
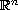 .
Using the improved Fourier
splitting method, we prove that a weak solution decays in
the
.
Using the improved Fourier
splitting method, we prove that a weak solution decays in
the
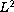 norm at the same rate as
norm at the same rate as
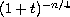 as the time
as the time
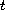 approaches infinity.
Also we obtain optimal
approaches infinity.
Also we obtain optimal
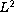 error-estimates
for Newtonian and Non-Newtonian flows.
error-estimates
for Newtonian and Non-Newtonian flows.
Submitted March 28, 2005. Published November 7, 2005.
Math Subject Classifications: 35B40, 35Q35, 76A05.
Key Words: Decay; bipolar non-Newtonian fluids;
Fourier splitting method.
Show me the
PDF file (259K),
TEX file for this article.
 |
Bo-Qing Dong
School of Mathematical Sciences
Nankai University
Tianjin 300071, China
email: bqdong@mail.nankai.edu.cn
|
|---|
Return to the EJDE web page
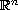 .
Using the improved Fourier
splitting method, we prove that a weak solution decays in
the
.
Using the improved Fourier
splitting method, we prove that a weak solution decays in
the
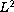 norm at the same rate as
norm at the same rate as
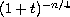 as the time
as the time
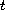 approaches infinity.
Also we obtain optimal
approaches infinity.
Also we obtain optimal
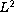 error-estimates
for Newtonian and Non-Newtonian flows.
error-estimates
for Newtonian and Non-Newtonian flows.
