Electron. J. Diff. Eqns.,
Vol. 2005(2005), No. 13, pp. 1-13.
Positive solutions to quasilinear equations involving
critical exponent on perturbed annular domains
Claudianor O. Alves
Abstract:
In this paper we study the existence of
positive solutions for the problem
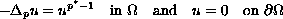
where
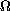 is a perturbed annular domain
(see definition in the introduction) and
is a perturbed annular domain
(see definition in the introduction) and
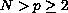 .
To prove our main results, we use the Concentration-Compactness
Principle and variational techniques.
.
To prove our main results, we use the Concentration-Compactness
Principle and variational techniques.
Submitted August 5, 2004. Published January 30, 2005.
Math Subject Classifications: 35B33, 35H30.
Key Words: p-Laplacian operator; critical exponents; deformation lemma
Show me the
PDF file (272K),
TEX file for this article.
 |
Claudianor O. Alves
Universidade Federal de Campina Grande
Departamento de Matemática e Estatística
CEP 58109-970 Campina Grande - PB, Brazil
email: coalves@dme.ufpb.br |
|---|
Return to the EJDE web page
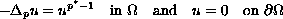
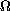 is a perturbed annular domain
(see definition in the introduction) and
is a perturbed annular domain
(see definition in the introduction) and
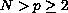 .
To prove our main results, we use the Concentration-Compactness
Principle and variational techniques.
.
To prove our main results, we use the Concentration-Compactness
Principle and variational techniques.
