Electron. J. Diff. Eqns., Vol. 2005(2005), No. 59, pp. 1-12.
Unique continuation property for the
Kadomtsev-Petviashvili (KP-II) equation
Mahendra Panthee
Abstract:
We generalize a method introduced by Bourgain in \cite{Borg} based on
complex analysis to address two spatial dimensional models and prove
that if a sufficiently smooth solution to the initial value problem
associated with the Kadomtsev-Petviashvili (KP-II) equation
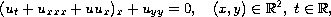
is supported compactly in a nontrivial time interval then
it vanishes identically.
Submitted April 9, 2005. Published June 10, 2005.
Math Subject Classifications: 35Q35, 35Q53
Key Words: Dispersive equations; KP equation; unique continuation property;
smooth solution; compact support.
Show me the
PDF file (267K),
TEX file for this article.
 |
Mahendra Panthee
Central Department of Mathematics
Tribhuvan University, Kirtipur, Kathmandu, Nepal
and Department of Mathematics
CMAGDS, IST, 1049-001
Av. Rovisco Pais, Lisbon, Portugal
email: mpanthee@math.ist.utl.pt |
|---|
Return to the EJDE web page