Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 05, pp. 1-12.
Asymptotic profile of a radially symmetric solution
with transition layers for an unbalanced bistable equation
Hiroshi Matsuzawa
Abstract:
In this article, we consider the semilinear elliptic problem
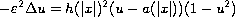
in
 with the Neumann boundary condition.
The function
with the Neumann boundary condition.
The function
 is a
is a
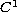 function satisfying
function satisfying
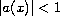 for
for
![$x\in [0,1]$](gifs/af.gif) and
and
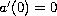 .
In particular we consider
the case
.
In particular we consider
the case
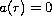 on some interval
on some interval
![$I\subset [0,1]$](gifs/ai.gif) .
The function
.
The function
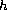 is a positive
is a positive
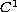 function satisfying
function satisfying
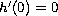 .
We investigate an asymptotic profile of the global minimizer
corresponding to the energy functional as
.
We investigate an asymptotic profile of the global minimizer
corresponding to the energy functional as
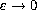 .
We use the variational procedure used in [4] with a few
modifications prompted by the presence of the function
.
We use the variational procedure used in [4] with a few
modifications prompted by the presence of the function
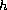 .
.
Submitted August 31, 2005. Published January 11, 2006.
Math Subject Classifications: 35B40, 35J25, 35J55, 35J50, 35K57.
Key Words: Transition layer; Allen-Cahn equation;
bistable equation; unbalanced.
Show me the
PDF file (257K),
TEX file for this article.
 |
Hiroshi Matsuzawa
Numazu National College of Technology
Ooka 3600, Numazu-city, Shizuoka 410-8501, Japan
email: hmatsu@numazu-ct.ac.jp |
|---|
Return to the EJDE web page
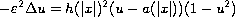
 with the Neumann boundary condition.
The function
with the Neumann boundary condition.
The function
 is a
is a
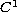 function satisfying
function satisfying
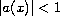 for
for
![$x\in [0,1]$](gifs/af.gif) and
and
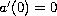 .
In particular we consider
the case
.
In particular we consider
the case
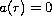 on some interval
on some interval
![$I\subset [0,1]$](gifs/ai.gif) .
The function
.
The function
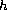 is a positive
is a positive
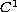 function satisfying
function satisfying
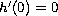 .
We investigate an asymptotic profile of the global minimizer
corresponding to the energy functional as
.
We investigate an asymptotic profile of the global minimizer
corresponding to the energy functional as
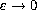 .
We use the variational procedure used in [4] with a few
modifications prompted by the presence of the function
.
We use the variational procedure used in [4] with a few
modifications prompted by the presence of the function
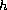 .
.
