Electron. J. Diff. Eqns., Vol. 2006(2006), No. 101, pp. 1-21.

BMO estimates near the boundary for solutions of elliptic systems

Azzeddine El Baraka

Abstract:
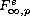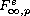In this paper we show that the scale of Sobolev-Campanato spaces $\mathcal{L}^{p,\lambda,s}$ contain the general BMO-Triebel-Lizorkin spaces $F_{\infty,p}^{s}$ as special cases, so that the conjecture by Triebel regarding estimates for solutions of scalar regular elliptic boundary value problems in $F_{\infty,p}^{s}$ spaces (solved in the case 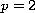$p=2$ in a previous work) is completely solved now. 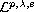Also we prove that the method used for the scalar case works for systems, and we give a priori estimates near the boundary for solutions of regular elliptic systems in the general spaces $\mathcal{L}^{p,\lambda,s}$ containing BMO, 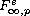$F_{\infty,p}^{s}$, and Morrey-Campanato spaces 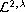$\mathcal{L}^{2,\lambda}$ as special cases. This result extends the work by the author in the scalar case.

Submitted March 2, 2006. Published August 31, 2006.
Math Subject Classifications: 35J45, 35J55.
Key Words: Elliptic systems; BMO-Triebel-Lizorkin spaces; Campanato spaces.

Show me the PDF file (319K), TEX file, and other files for this article.

Azzeddine El Baraka
University Sidi Mohamed Ben Abdellah
FST Fez, BP 2202, Route Immouzer
30000 Fez, Morocco
email: aelbaraka@yahoo.com

Return to the EJDE web page