Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 129, pp. 1-12.
Existence of positive solutions for multi-term non-autonomous
fractional differential equations with polynomial coefficients
Azizollah Babakhani, Varsha Daftardar-Gejji
Abstract:
In the present paper we discuss the existence of positive solutions
in the case of multi-term non-autonomous fractional differential equations
with polynomial coefficients; the constant coefficient case has been
studied in [2]. We consider the equation

We state various conditions on
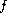 and
and
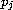 's under which
this equation has: positive solutions, a unique solution which is positive,
and a unique solution which may not be positive.
's under which
this equation has: positive solutions, a unique solution which is positive,
and a unique solution which may not be positive.
Submitted July 27, 2005. Published October 16, 2006.
Math Subject Classifications: 26A33, 34B18.
Key Words: Riemann-Liouville fractional derivatives and integrals;
normal cone; semi-ordered Banach space;
completely continuous operator; equicontinuous set.
Show me the
PDF file (252K),
TEX file for this article.
 |
Azizollah Babakhani
Department of Mathematics
University of Mazanderan, Babol, Iran
email: babakhani@nit.ac.ir |
|---|
 |
Varsha Daftardar-Gejji
Department of Mathematics, University of Pune
Ganeshkhind, Pune - 411007, India
email: vsgejji@math.unipune.ernet.in |
|---|
Return to the EJDE web page

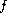 and
and
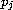 's under which
this equation has: positive solutions, a unique solution which is positive,
and a unique solution which may not be positive.
's under which
this equation has: positive solutions, a unique solution which is positive,
and a unique solution which may not be positive.

