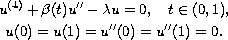Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 100, pp. 1-8.
Multiplicity results for fourth-order boundary-value problem at
resonance with variable coefficients
Ling Xu
Abstract:
This paper studies the multiplicity of solutions for the fourth-order
boundary value problem at resonance with variable coefficients
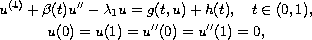
where
![$\beta\in C[0,1]$](gifs/ab.gif) with
with
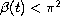 on
on
![$[0,1]$](gifs/ad.gif) ,
,
![$g:[0, 1]\times \mathbb{R}\to \mathbb{R}$](gifs/ae.gif) is bounded
continuous function,
is bounded
continuous function,
 and
and
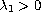 is the
first eigenvalue of the associated linear homogeneous boundary value
problem
is the
first eigenvalue of the associated linear homogeneous boundary value
problem
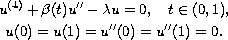
The proof of our main result is based on the connectivity
properties of the solution sets of parameterized families of compact
vector fields.
Submitted April 14, 2008. Published July 30, 2008.
Math Subject Classifications: 39A10.
Key Words: Connected subsets; resonance; multiplicity results.
Show me the
PDF file (220 KB),
TEX file for this article.
 |
Ling Xu
College of Mathematics and Information Science
Northwest Normal University
Lanzhou, Gansu 730070, China
email: xuling_216@yahoo.cn |
|---|
Return to the EJDE web page
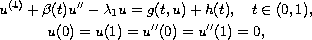
![$\beta\in C[0,1]$](gifs/ab.gif) with
with
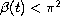 on
on
![$[0,1]$](gifs/ad.gif) ,
,
![$g:[0, 1]\times \mathbb{R}\to \mathbb{R}$](gifs/ae.gif) is bounded
continuous function,
is bounded
continuous function,
 and
and
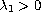 is the
first eigenvalue of the associated linear homogeneous boundary value
problem
is the
first eigenvalue of the associated linear homogeneous boundary value
problem