Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 105, pp. 1-8.
A Riccati technique for proving oscillation of a half-linear equation
Pavel Rehak
Abstract:
In this paper we study the oscillation of solutions to
the half-linear differential equation
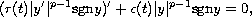
under the assumptions
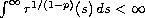 ,
,
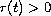 ,
,
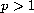 .
Our main tool is a Riccati type transformation for using the
so called "function sequence technique".
This method leads to new and to known oscillation and comparison
results. We also give an example that illustrates our results.
.
Our main tool is a Riccati type transformation for using the
so called "function sequence technique".
This method leads to new and to known oscillation and comparison
results. We also give an example that illustrates our results.
Submitted May 12, 2008. Published August 6, 2008.
Math Subject Classifications: 34C10.
Key Words: Half-linear differential equation; Riccati technique;
oscillation criteria.
Show me the
PDF file (210 KB),
TEX file for this article.
 |
Pavel Rehak
Institute of Mathematics, Academy of Sciences
Zizkova 22, CZ61662 Brno, Czech Republic
email: rehak@math.muni.cz |
|---|
Return to the EJDE web page
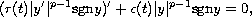
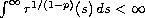 ,
,
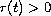 ,
,
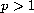 .
Our main tool is a Riccati type transformation for using the
so called "function sequence technique".
This method leads to new and to known oscillation and comparison
results. We also give an example that illustrates our results.
.
Our main tool is a Riccati type transformation for using the
so called "function sequence technique".
This method leads to new and to known oscillation and comparison
results. We also give an example that illustrates our results.
