Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 158, pp. 1-16.
Existence of nonnegative solutions to positone-type problems
in R^N with indefinite weights
Dhanya Rajendran, Jagmohan Tyagi
Abstract:
We study the existence of a nonnegative solution to the following
problem in
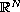 ,
,
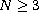 ,
in both the radial as well as in the
non-radial case with an indefinite weight function
,
in both the radial as well as in the
non-radial case with an indefinite weight function
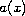 :
:

The nonlinearity f above is of "positone" type; i.e., f is
monotone increasing with
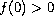 .
We show the existence of a
nonnegative solution to the above problem for
.
We show the existence of a
nonnegative solution to the above problem for
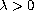 small enough.
We also prove the existence of a nonnegative solution to the above
problem in exterior as well as in annular domains. Motivated by the
scalar equation, we further extend these results to the case of
coupled system. Our proof involves the method of monotone iteration
applied to the integral equation corresponding to the problem.
small enough.
We also prove the existence of a nonnegative solution to the above
problem in exterior as well as in annular domains. Motivated by the
scalar equation, we further extend these results to the case of
coupled system. Our proof involves the method of monotone iteration
applied to the integral equation corresponding to the problem.
Submitted January 16, 2010. Published November 4, 2010.
Math Subject Classifications: 35J45, 35J55.
Key Words: Elliptic system; nonnegative solution; existence of solutions.
Show me the PDF file (289 KB),
TEX file, and other files for this article.
| |
Dhanya Rajendran
TIFR Centre For Applicable Mathematics,
Post Bag No. 6503, Sharda Nagar
Chikkabommasandra, Bangalore-560065, Karnataka, India
email: dhanya@math.tifrbng.res.in
|
|---|
 |
Jagmohan Tyagi
TIFR Centre For Applicable Mathematics,
Post Bag No. 6503, Sharda Nagar
Chikkabommasandra, Bangalore-560065, Karnataka, India
email: jtyagi1@gmail.com
|
|---|
Return to the EJDE web page
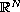 ,
,
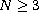 ,
in both the radial as well as in the
non-radial case with an indefinite weight function
,
in both the radial as well as in the
non-radial case with an indefinite weight function
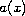 :
:

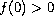 .
We show the existence of a
nonnegative solution to the above problem for
.
We show the existence of a
nonnegative solution to the above problem for
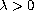 small enough.
We also prove the existence of a nonnegative solution to the above
problem in exterior as well as in annular domains. Motivated by the
scalar equation, we further extend these results to the case of
coupled system. Our proof involves the method of monotone iteration
applied to the integral equation corresponding to the problem.
small enough.
We also prove the existence of a nonnegative solution to the above
problem in exterior as well as in annular domains. Motivated by the
scalar equation, we further extend these results to the case of
coupled system. Our proof involves the method of monotone iteration
applied to the integral equation corresponding to the problem.
