Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 27, pp. 1-7.
Exact multiplicity of solutions for a class of
two-point boundary value problems
Yulian An, Ruyun Ma
Abstract:
We consider the exact multiplicity of nodal solutions of the
boundary value problem
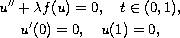
where
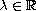 is a positive parameter.
is a positive parameter.
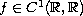 satisfies
satisfies
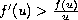 , if
, if
 .
There exist
.
There exist
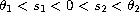 such that
such that
 ;
;
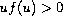 , if
, if
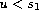 or
or
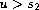 ;
;
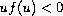 ,
if
,
if
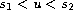 and
and
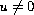 ;
;
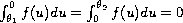 . The limit
. The limit
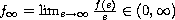 .
Using bifurcation techniques and the Sturm comparison theorem,
we obtain curves of solutions which bifurcate from infinity at the
eigenvalues of the corresponding linear problem, and obtain the
exact multiplicity of solutions to the problem for
.
Using bifurcation techniques and the Sturm comparison theorem,
we obtain curves of solutions which bifurcate from infinity at the
eigenvalues of the corresponding linear problem, and obtain the
exact multiplicity of solutions to the problem for
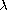 lying
in some interval in
lying
in some interval in
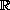 .
.
Submitted September 30, 2009. Published February 16, 2010.
Math Subject Classifications: 34B15, 34A23.
Key Words: Exact multiplicity; nodal solutions; bifurcation from infinity;
linear eigenvalue problem.
Show me the PDF file (222 KB),
TEX file for this article.
 |
Yulian An
Department of Mathematics
Shanghai Institute of Technology
shanghai 200235, China
email: an_yulian@tom.com |
|---|
 |
Ruyun Ma
Department of Mathematics
Northwest Normal University
Lanzhou 730070, Gansu, China
email: mary@nwnu.edu.cn |
Return to the EJDE web page
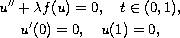
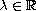 is a positive parameter.
is a positive parameter.
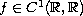 satisfies
satisfies
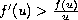 , if
, if
 .
There exist
.
There exist
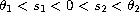 such that
such that
 ;
;
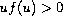 , if
, if
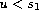 or
or
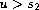 ;
;
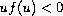 ,
if
,
if
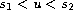 and
and
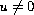 ;
;
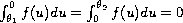 . The limit
. The limit
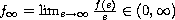 .
Using bifurcation techniques and the Sturm comparison theorem,
we obtain curves of solutions which bifurcate from infinity at the
eigenvalues of the corresponding linear problem, and obtain the
exact multiplicity of solutions to the problem for
.
Using bifurcation techniques and the Sturm comparison theorem,
we obtain curves of solutions which bifurcate from infinity at the
eigenvalues of the corresponding linear problem, and obtain the
exact multiplicity of solutions to the problem for
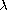 lying
in some interval in
lying
in some interval in
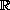 .
.

