Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 37, pp. 1-5.
An inverse boundary-value problem for semilinear elliptic
equations
Ziqi Sun
Abstract:
We show that in dimension two or greater, a certain equivalence
class of the scalar coefficient
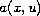 of the semilinear elliptic
equation
of the semilinear elliptic
equation
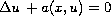 is uniquely determined by
the Dirichlet to Neumann map of the equation on a
bounded domain with smooth boundary. We also show that
the coefficient
is uniquely determined by
the Dirichlet to Neumann map of the equation on a
bounded domain with smooth boundary. We also show that
the coefficient
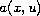 can be determined by the Dirichlet to Neumann
map under some additional hypotheses.
can be determined by the Dirichlet to Neumann
map under some additional hypotheses.
Submitted January 31, 2010. Published March 14, 2010.
Math Subject Classifications: 35R30.
Key Words: Inverse Problem; Dirichlet to Neumann map.
Show me the PDF file (175 KB),
TEX file for this article.
 |
Ziqi Sun
Department of Mathematics and Statistics
Wichita State University, Wichita, KS 67260-0033, USA
email: ziqi.sun@wichita.edu |
|---|
Return to the EJDE web page
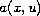 of the semilinear elliptic
equation
of the semilinear elliptic
equation
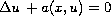 is uniquely determined by
the Dirichlet to Neumann map of the equation on a
bounded domain with smooth boundary. We also show that
the coefficient
is uniquely determined by
the Dirichlet to Neumann map of the equation on a
bounded domain with smooth boundary. We also show that
the coefficient
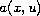 can be determined by the Dirichlet to Neumann
map under some additional hypotheses.
can be determined by the Dirichlet to Neumann
map under some additional hypotheses.
