Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 164, pp. 1-8.
Existence of positive solutions for semilinear elliptic
systems with indefinite weight
Ruipeng Chen
Abstract:
This article concerns the existence of positive solutions
of semilinear elliptic system
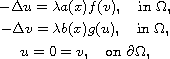
where
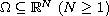 is a bounded
domain with a smooth boundary
is a bounded
domain with a smooth boundary
 and
and
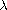 is a
positive parameter.
is a
positive parameter.
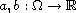 are sign-changing
functions.
are sign-changing
functions.
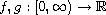 are continuous with
are continuous with
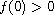 ,
,
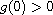 .
By applying Leray-Schauder fixed point theorem,
we establish the existence of positive solutions for
.
By applying Leray-Schauder fixed point theorem,
we establish the existence of positive solutions for
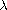 sufficiently small.
sufficiently small.
Submitted September 13, 2011. Published December 13, 2011.
Math Subject Classifications: 35J45.
Key Words: Semilinear elliptic systems; indefinite weight;
positive solutions; existence of solutions.
Show me the PDF file (209 KB),
TEX file for this article.
 |
Ruipeng Chen
Department of Mathematics
Northwest Normal University
Lanzhou, 730070, China
email: ruipengchen@126.com
|
|---|
Return to the EJDE web page
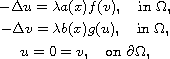
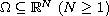 is a bounded
domain with a smooth boundary
is a bounded
domain with a smooth boundary
 and
and
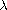 is a
positive parameter.
is a
positive parameter.
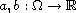 are sign-changing
functions.
are sign-changing
functions.
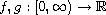 are continuous with
are continuous with
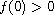 ,
,
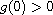 .
By applying Leray-Schauder fixed point theorem,
we establish the existence of positive solutions for
.
By applying Leray-Schauder fixed point theorem,
we establish the existence of positive solutions for
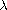 sufficiently small.
sufficiently small.
