Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 69, pp. 1-33.
The Legendre equation and its self-adjoint operators
Lance L. Littlejohn, Anton Zettl
Abstract:
The Legendre equation has interior singularities at -1 and +1.
The celebrated classical Legendre polynomials are the eigenfunctions
of a particular self-adjoint operator in
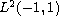 .
We characterize all self-adjoint Legendre operators in
.
We characterize all self-adjoint Legendre operators in
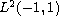 as well as those in
as well as those in
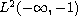 and in
and in
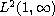 and discuss their spectral properties. Then, using the
"three-interval theory", we find all self-adjoint Legendre operators
in
and discuss their spectral properties. Then, using the
"three-interval theory", we find all self-adjoint Legendre operators
in
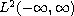 .
These include operators which are not
direct sums of operators from the three separate intervals and thus
are determined by interactions through the singularities at -1
and +1.
.
These include operators which are not
direct sums of operators from the three separate intervals and thus
are determined by interactions through the singularities at -1
and +1.
Submitted April 17, 2011. Published May 25, 2011.
Math Subject Classifications: 05C38, 15A15, 05A15, 15A18.
Key Words: Legendre equation; self-adjoint operators;
spectrum; three-interval problem.
Show me the PDF file (416 KB),
TEX file for this article.
 |
Lance L. Littlejohn
Department of Mathematics, Baylor University
One Bear Place # 97328, Waco, TX 76798-7328, USA
email: lance_littlejohn@baylor.edu
|
|---|
 |
Anton Zettl
Department of Mathematical Sciences
Northern Illinois University
DeKalb, IL 60115-2888, USA
email: zettl@math.niu.edu
|
|---|
Return to the EJDE web page
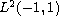 .
We characterize all self-adjoint Legendre operators in
.
We characterize all self-adjoint Legendre operators in
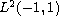 as well as those in
as well as those in
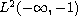 and in
and in
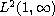 and discuss their spectral properties. Then, using the
"three-interval theory", we find all self-adjoint Legendre operators
in
and discuss their spectral properties. Then, using the
"three-interval theory", we find all self-adjoint Legendre operators
in
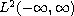 .
These include operators which are not
direct sums of operators from the three separate intervals and thus
are determined by interactions through the singularities at -1
and +1.
.
These include operators which are not
direct sums of operators from the three separate intervals and thus
are determined by interactions through the singularities at -1
and +1.

