This article concerns the existence of solutions to the nonlinear fractional boundary-value problem
![$$\displaylines{
\frac{d}{dt} \Big({}_0 D_t^{\alpha-1}({}_0^c D_t^{\alpha} u(t))
-{}_t D_T^{\alpha-1}({}_t^c D_T^{\alpha} u(t))\Big)
+\lambda f(u(t)) = 0, \quad\hbox{a.e. } t \in [0, T], \cr
u(0) = u(T) = 0,
}$$](gifs/aa.gif)
where
![$\alpha \in (1/2, 1]$](gifs/ab.gif)
,
and
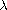is a positive real parameter.
The approach is based on a local minimum theorem established by Bonanno.
Chuanzhi Bai
Abstract:
This article concerns the existence of solutions to the nonlinear
fractional boundary-value problem
where
,
and
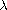is a positive real parameter.
The approach is based on a local minimum theorem established by Bonanno.
Submitted July 30, 2012. Published October 12, 2012.
Math Subject Classifications: 58E05, 34B15, 26A33.
Key Words: Critical points; fractional differential equations;
boundary-value problem.
Show me the PDF file (227 KB), TEX file, and other files for this article.
 |
Chuanzhi Bai Department of Mathematics Huaiyin Normal University Huaian, Jiangsu 223300, China email: czbai8@sohu.com |
|---|
Return to the EJDE web page