Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 160, pp. 1-16.
Solvability in the sense of sequences to some non-Fredholm operators
Vitaly Volpert, Vitali Vougalter
Abstract:
We study the solvability of certain linear nonhomogeneous
elliptic problems and show that under reasonable technical conditions the
convergence in
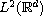 of their right sides implies the
existence and the convergence in
of their right sides implies the
existence and the convergence in
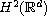 of the solutions. The
equations involve second order differential operators without Fredholm
property and we use the methods of spectral and scattering theory for
Schrodinger type operators analogously to our preceding work [17].
of the solutions. The
equations involve second order differential operators without Fredholm
property and we use the methods of spectral and scattering theory for
Schrodinger type operators analogously to our preceding work [17].
Submitted March 8, 2013. Published July 12, 2013.
Math Subject Classifications: 35J10, 35P10, 47F05
Key Words: Solvability conditions; non Fredholm operators; Sobolev spaces.
Show me the PDF file (291 KB),
TEX file for this article.
 |
Vitaly Volpert
Institute Camille Jordan, UMR 5208 CNRS,
University Lyon 1
Villeurbanne, 69622, France.
Department of Mathematics, Mechanics and Computer Science
Southern Federal University Rostov-on-Don, Russia
email: volpert@math.univ-lyon1.fr
|
|---|
 |
Vitali Vougalter
Department of Mathematics and Applied Mathematics
University of Cape Town
Private Bag, Rondebosch 7701, South Africa
email: Vitali.Vougalter@uct.ac.za
|
|---|
Return to the EJDE web page
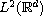 of their right sides implies the
existence and the convergence in
of their right sides implies the
existence and the convergence in
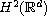 of the solutions. The
equations involve second order differential operators without Fredholm
property and we use the methods of spectral and scattering theory for
Schrodinger type operators analogously to our preceding work [17].
of the solutions. The
equations involve second order differential operators without Fredholm
property and we use the methods of spectral and scattering theory for
Schrodinger type operators analogously to our preceding work [17].

