In this article, we study the bifurcation of limit cycles from the linear oscillator
 ,
,
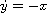 in the class
in the class
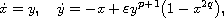
where
 is a small positive parameter tending to 0,
is a small positive parameter tending to 0,
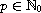 is even and
is even and
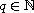 .
We prove that the above differential system, in the global plane
where
.
We prove that the above differential system, in the global plane
where
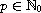 is even and
is even and
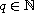 ,
has a unique limit cycle. More specifically, the existence
of a limit cycle, which is the main result in this work,
is obtained by using the Poincare's method, and the uniqueness
can be derived from the work of Sabatini and Villari [6].
We also investigate and some other properties of this unique
limit cycle for some special cases of this differential system.
Such special cases have been studied by Minorsky [3] and
Moremedi et al [4].
,
has a unique limit cycle. More specifically, the existence
of a limit cycle, which is the main result in this work,
is obtained by using the Poincare's method, and the uniqueness
can be derived from the work of Sabatini and Villari [6].
We also investigate and some other properties of this unique
limit cycle for some special cases of this differential system.
Such special cases have been studied by Minorsky [3] and
Moremedi et al [4].
